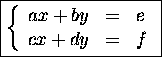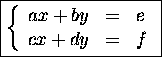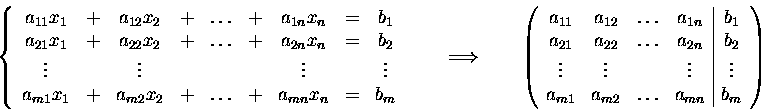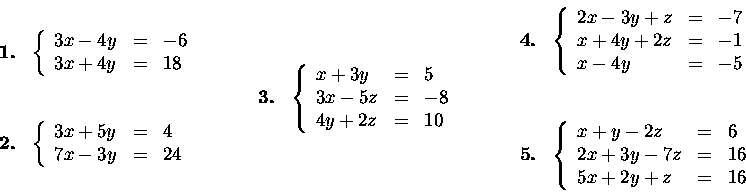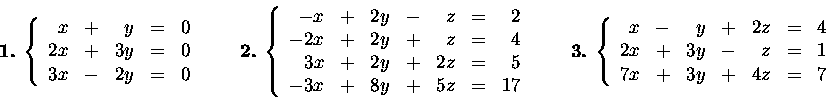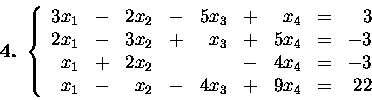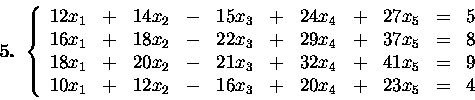LINEAR ALGEBRA (Math 211)
Sheet #1

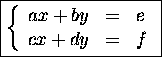
Systems of two linear equations in two variables. \fbox{$\left\{\begin{array}{lcl} ax+by &=& e\\ cx+dy &=& f \end{array}\right.$}


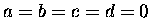if $\displaystyle a=b=c=d=0$
then
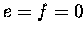if $\displaystyle e=f=0$
then the system has infinitely many solutions
else the systems is inconsistent (there is no any solution)


else
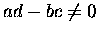if $\displaystyle ad-bc \not= 0$
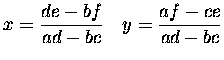then the system has a unique solution: $\displaystyle x={de-bf\over ad-bc}\quad y={af-ce\over ad-bc}$
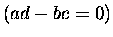else $\displaystyle (ad-bc=0)$
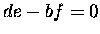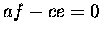
if $\displaystyle de-bf=0$ and $\displaystyle af-ce=0$
then the system has infinitely many solutions
else the systems is inconsistent




Augmented matrix.

\begin{displaymath}\left\{\begin{array}{ccccccccc} a_{11}x_1&+&a_{12}x_2&+&\dots... ...s&\vdots \\ a_{m1}&a_{m2}&\dots&a_{mn}&b_m \end{array}\right)\end{displaymath}



Gaussian elimination.

1.
Locate the leftmost column in the matrix of the system that does not consist entirely of zeroes.

2.
Interchange the top row with another row, if necessary, to bring a nonzero entry to the top of the column found in Step 1.

3.
if the entry that is now at the top of the column found in Step 1 is a, multiply the first row by 1/a in order to introduce a leading 1.

4.
Add suitable multiplies of the top row to the rows below so that all entries below leading 1 become zeroes.

5.
Forget about the top row in the matrix and begin again with Step 1 applied to the remaining submatrix. Continue in this way until there are no more nonzero rows in the submatrix.

6.
Begin with the last nonzero row and working upward, add suitable multiples of each row to the rows above to introduce zeros above the leading 1's.

7.
Solve the equations for the leading variables, and aasign arbitrary values to any nonleading variables.




LINEAR ALGEBRA (Math 211)
HW #1 (Due Mon. Sept. 18)


Solve the following systems of linear equations

\begin{displaymath}\begin{array}{lll} \begin{array}{ll} \mbox{\bf 1.} & \left\{\... ...6\\ 5x+2y+z &=& 16 \end{array}\right. \end{array}\end{array}\end{displaymath}









LINEAR ALGEBRA (Math 211)
HW #2 (Due Wed. Sept. 20)


Find all solutions of the following systems by Gaussian elimination method.

\begin{displaymath}\mbox{\bf 1.}\ \left\{ \begin{array}{rcrcr} x &+&y &=& 0\\ ... ...\\ 2x&+&3y&-& z&=& 1\\ 7x&+&3y&+&4z&=& 7 \end{array}\right.\end{displaymath}




\begin{displaymath}\mbox{\bf 4.}\ \left\{ \begin{array}{rcrcrcrcr} 3x_1&-&2x_2... ...&4x_4&=&-3\\ x_1&-& x_2&-&4x_3&+&9x_4&=&22 \end{array}\right.\end{displaymath}




\begin{displaymath}\mbox{\bf 5.}\ \left\{ \begin{array}{rcrcrcrcrcr} 12x_1&+&... ... 10x_1&+&12x_2&-&16x_3&+&20x_4&+&23x_5&=& 4 \end{array}\right.\end{displaymath}