LINEAR ALGEBRA (Math 211)
Sheet #2

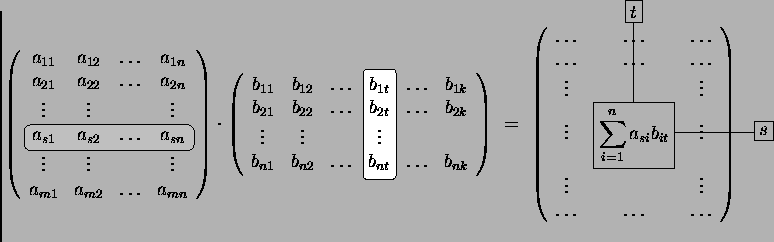
Multiplication of matrices. \fbox{${\cal M}(m,n)\times {\cal M}(n,k) \to {\cal M}(m,k)$}


\begin{displaymath}\begin{picture} (500,140)(0,0) \put(12,56){\epsfxsize=108pt ... ...95,87){\line(0,1){50}} \put(390,140){\fbox{$t$}} \end{picture}\end{displaymath}


Matrix representation of a linear system:         \fbox{$A\cdot X=B$}

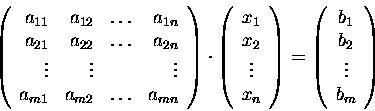
\begin{displaymath}\left(\begin{array}{rrrr} a_{11}&a_{12}&\dots&a_{1n}\\ a_{21... ...ft(\begin{array}{c} b_1\\ b_2 \\ \vdots\\ b_m\end{array}\right)\end{displaymath}

Indentity matrix: $\displaystyle I=\left(\begin{array}{cccc} 1&0&\dots&0\\ 0&1&\dots&0\\ \vdots&\vdots& &\vdots\\ 0&0&\dots&1 \end{array}\right) \in {\cal M}(n,n)$.
Inverse matrix: \fbox{$A\cdot A^{-1} = A^{-1}\cdot A =I$}

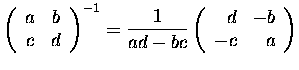$\displaystyle \left(\begin{array}{cc} a&b\\ c&d \end{array}\right)^{-1} = {1\over ad-bc} \left(\begin{array}{rr} d&-b\\ -c&a \end{array}\right)$


Solving a sytem $A\cdot X=B$ of n linear equations of n variables:         \fbox{$X= A^{-1}\cdot B$}




An elementary matrix is a matrix which can be obtained from an identity matrix by one of the following tree operations:

$\textstyle \parbox{10cm}{ {\bf (1)} Multiply a row by a nonzero constant.\\ {\... ...} Interchange two rows.\\ {\bf (3)} Add a multiple of one row to another row.}$

Theorem. If E is an elementary matrix then the matrix $E\cdot A$ is obtained from matrix A by the row operation (1)-(3) corrsponding to E.



Examples.

$\left(\begin{array}{rr} -5&0\\ 0&1 \end{array}\right)$
  $\left(\begin{array}{rrrr} 0&0&1&0\\ 0&1&0&0\\ 1&0&0&0\\ 0&0&0&1 \end{array}\right)$   $\left(\begin{array}{rrr} 1&0&0\\ 0&1&0\\ 7&0&1 \end{array}\right)$
$\uparrow$  $\uparrow$  $\uparrow$
Multiplication of the first row by -5  Interchanging of the first and third rows  Addition 7 times the first row to the third row


A method for inverting matrices.

$\bullet$ Adjoin the identity matrix I to the right side of A producing $\left( A \vert I \right)$.

$\bullet$ Apply row operations (1)-(3) to this matrix until the left half is reduced to I. The right half will be converted into the inverse matrix: $\left( I \vert A^{-1} \right)$.

LINEAR ALGEBRA (Math 211)
HW #3 (Due Mon. Sept. 25 )


Multiply the following matrices.

1. $\left(\begin{array}{rr} 1&2\\ 3&4 \end{array}\right)\cdot\left(\begin{array}{rr} 5&6\\ 7&8 \end{array}\right) =\ ?$ 2. $\left(\begin{array}{rrrr} 9&-3&5&6\\ 6&-2&3&4\\ 3&-1&3&14 \end{array}\right)\cdot\left(\begin{array}{r} 2\\ -7\\ -7\\ 0 \end{array}\right) =\ ?$


Find the following inverses.

3. $\left(\begin{array}{rr} \cos\alpha & \sin\alpha\\ -\sin\alpha& \cos\alpha \end{array}\right)^{-1} =\ ?$


4. $\left(\begin{array}{rrr} 1&0&1\\ 1&1&0\\ 1&1&1 \end{array}\right)^{-1} =\ ?$
5. $\left(\begin{array}{rrrr} a_{11}& 0&\dots&0\\ 0&a_{22}&\dots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0& 0&\dots&a_{nn} \end{array}\right)^{-1} =\ ?$, if $a_{11}\cdot a_{22}\cdot\dots\cdot a_{nn}\not= 0$.









LINEAR ALGEBRA (Math 211)
HW #4 (Due Wed. Sept. 27)


Find the following inverses and their representation as the product of elementary matrices.

1. $\left(\begin{array}{rr} -3& 8\\ -1& 3 \end{array}\right)^{-1}$ 2. $\left(\begin{array}{rr} 7& 9\\ -6&-8 \end{array}\right)^{-1}$




Find the inverses.

3. $\left(\begin{array}{rrr} 2&7&3\\ 3&9&4\\ 1&5&3 \end{array}\right)^{-1}$ 4. $\left(\begin{array}{rrrrr} 1&1&1&\dots&1\\ 0&1&1&\dots&1\\ 0&0&1&\dots&1\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\dots&1 \end{array}\right)^{-1}$


5. Solve matrix equation         $\left(\begin{array}{rr} 3&-1\\ 5&-2 \end{array}\right)\cdot X\cdot \left(\begi... ...\end{array}\right) = \left(\begin{array}{rr} 14&16\\ 9&10 \end{array}\right)$