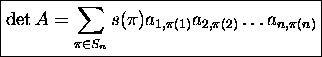LINEAR ALGEBRA (Math 211)
Sheet #3
DETERMINANTS

Axiomatic definition.

The determinant is a function $\det: {\cal M}(n,n) \to {\mathbb R}$ satisfying the following axioms:

(i)
multilinear function of rows:
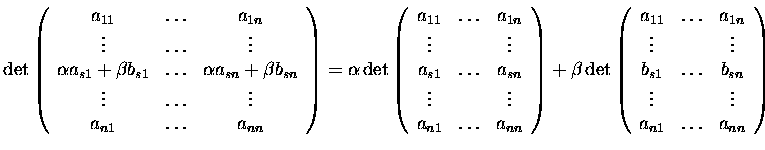
$\det\left(\begin{array}{ccc} a_{11}&\dots&a_{1n}\\ \vdots&\dots&\vdots\\ {\al... ..._{s1}&\dots&b_{sn}\\ \vdots& &\vdots\\ a_{n1}&\dots&a_{nn} \end{array}\right)$

(ii)
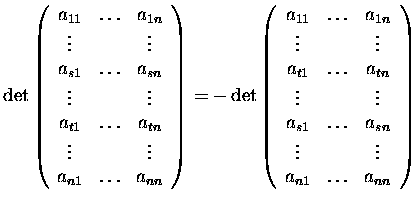
skew-symmetric function of rows: $\det\left(\begin{array}{ccc} a_{11}&\dots&a_{1n}\\ \vdots& &\vdots\\ a_{s1}&\... ..._{s1}&\dots&a_{sn}\\ \vdots& &\vdots\\ a_{n1}&\dots&a_{nn} \end{array}\right)$

(iii)
normalization: $\det(I)=1$



Examples.

\fbox{$n=2$}

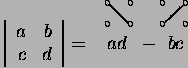
\begin{displaymath}\left\vert\begin{array}{rr} a&b\\ c&d \end{array}\right\vert... ...}}} \put(8,-4){\line(1,1){12}} \end{picture}}} \end{picture}}\end{displaymath}


\fbox{$n=3$}

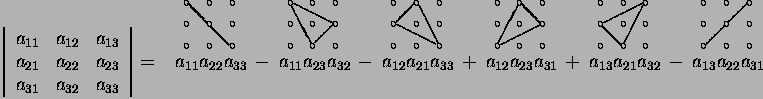
\begin{displaymath}\left\vert\begin{array}{rrr} a_{11}&a_{12}&a_{13}\\ a_{21}&a... ...12}} \put(22,3){\line(1,1){12}} \end{picture}}} \end{picture}}\end{displaymath}



Permutations. A permutation is a one-to-one correspondence between numeres 1, 2, ..., n.

\begin{displaymath}\pi =\left(\begin{array}{cccc} 1&2&\dots&n\\ \downarrow&\dow... ...\fbox{Short notation: $\pi = (\pi(1), \pi(2), \dots, \pi(n))$}\end{displaymath}

Example. All permutations of {1, 2, 3} are (1, 2, 3) (1,3,2) (2,1,3) (2,3,1) (3,1,2) (3,2,1).


Product: \fbox{$\pi'\cdot\pi = \left(\pi'(\pi(1)), \pi'(\pi(2)), \dots, \pi'(\pi(n))\right)$}          $(3, 1, 2)\cdot (2,3,1) = (1, 2, 3) $


Sn is the group of all permutations of the set $\{1, 2, \dots, n\}$.          \fbox{$\left\vert S_n\right\vert = n!$}


An inversion in a permutation $\pi$ is a pair i,j such that i<j but $\pi(i) > \pi(j)$.


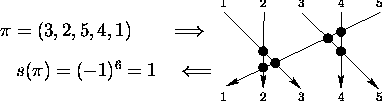
A sign of a permutation. $s(\pi) = (-1)^{\char93 \{\mbox{\scriptsize of inversions in } \pi\}} = (-1)^{\char93 \{\mbox{\scriptsize number of intersections of lines in a picture}\}}$




\fbox{$\displaystyle \det A = \sum_{\pi\in S_n} s(\pi) a_{1,\pi(1)}a_{2,\pi(2)}\dots a_{n,\pi(n)}$}          \begin{picture} (200,10)(0,0) \put(0,5){\mbox{$\pi=(3, 2, 5, 4,1)\qquad \Longri... ...e 5$}} \put(10,-20){\mbox{$s(\pi)=(-1)^6=1\quad \Longleftarrow$}} \end{picture}