LINEAR ALGEBRA (Math 211)
HW #7 (Due Wed. Oct. 18 )

1. For matrix $A=\left(\begin{array}{rrrr} 1&2&1&3\\ 4&-1&5&-1\\ \end{array}\right)$ compute $\mbox{({\bf a})\ } A\cdot A^T \qquad \mbox{({\bf b})\ } A^T\cdot A$.


2. Let A and B be 3 x 3 matrices with $\det A= 4$ and $\det B= 5$. Find the value of

\begin{displaymath}\mbox{({\bf a})\ } \det(AB) \qquad \mbox{({\bf b})\ } \det(3... ...({\bf c})\ } \det(2AB) \qquad \mbox{({\bf d})\ } \det(A^{-1}B)\end{displaymath}


3. Let E1, E2, E3 be 3 x 3 elementary matrices of types (1), (2), and (3), respectively, and let A be a 3 x 3 matrices with $\det A = 6$. Assume, additionally, that E1 corresponds to multiplication of the second row by 3. Find the values of each of the following

\begin{displaymath}\mbox{({\bf a})\ } \det(E_1A) \quad \mbox{({\bf b})\ } \det(... ...bf e})\ } \det(E_2^2) \quad \mbox{({\bf f})\ } \det(E_1E_2E_3)\end{displaymath}


4. Assuming that 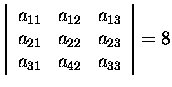$\left\vert\begin{array}{rrr} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{42}&a_{33} \end{array}\right\vert=8$ compute the following determinants

\begin{displaymath}\mbox{({\bf a})\ }\left\vert\begin{array}{rrr} a_{31}&a_{42}... ...&a_{42}&a_{33}\\ a_{21}&a_{22}&a_{23} \end{array}\right\vert\end{displaymath}


5.

(a) A matrix A is said to be idempotent if A2=A. Prove that if A is idempotent, then $\det A =0$ or 1.

(b) A matrix A is said to be nilpotent if Ak=0 for some positive integer k. Prove that if A is nilpotent, then $\det A =0$.

(c) A matrix A is said to be orthogonal if $A\cdot A^T=I$. Prove that if A is orthogonal, then $\det A =1$ or -1.

(d) An n x n matrix A is said to be skew symmetric if AT=-A. Prove that if A is sew symmetric and n is odd, then $\det A =0$.