LINEAR ALGEBRA (Math 211)
Sheet #4
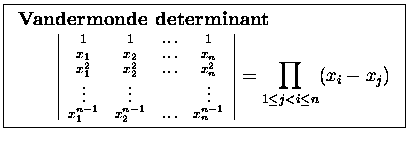
DETERMINANTS 2
Transpose of a matrix.
Product and inverse.
Theorem. A matrix A is invertible if and only if 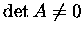 .
.
Theorem. (Evaluating determinants by row reduction)
(1) If a row (or a column) of A is multiplied by a constant 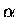 ,
then
,
then 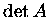 is multiplied by
is multiplied by 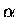 .
.
(2) Interchanging any two rows (or columns) of A changes the sign
of 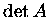 .
.
(3) If a multiple of one row (column) of A is added to another
row (column) of A, then the determinant is unchanged.
Eigenvalues and eigenvectors
Definition. An eigenvalue of a matrix A is a value of 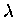 such that the matrix
such that the matrix 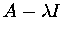 is not invertible (roots of the
characteristic equation
is not invertible (roots of the
characteristic equation
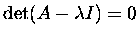 ).
).
Definition. An eigenvector corresponding to an eigenvalue 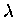 of a matrix A is a nontrivial solution of the system
of a matrix A is a nontrivial solution of the system
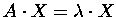
Definition. Let A=(aij) be a square matrix. The minor
Mij of
an entry aij is the determinant of the matrix obtained from A by
deleting the i-th row and j-th column. The number
Cij=(-1)i+jMij is called the cofactor of antry aij.
Theorem. (Cofactor expansion)
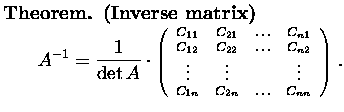
Cramer's rule.

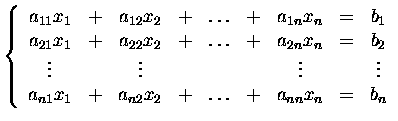 has a unique solution
has a unique solution
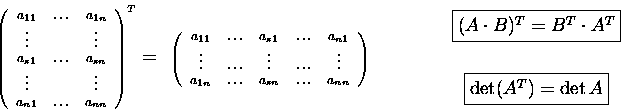
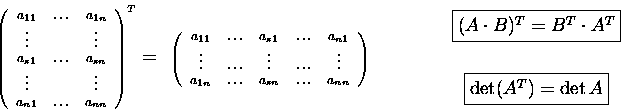
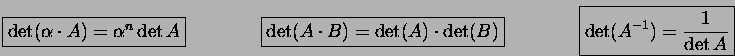
![]() of a matrix A is a nontrivial solution of the system
of a matrix A is a nontrivial solution of the system
![]()
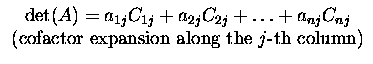
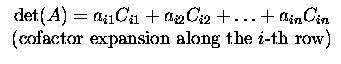
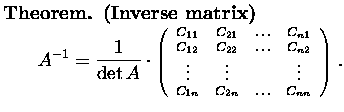


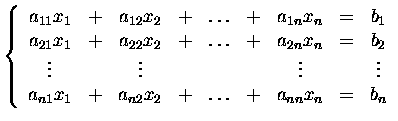 has a unique solution
has a unique solution
