LINEAR ALGEBRA (Math 211)
Sheet #5
\fbox{{\Large\bf ${\mathbb R}^n$}}

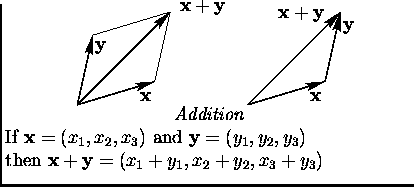
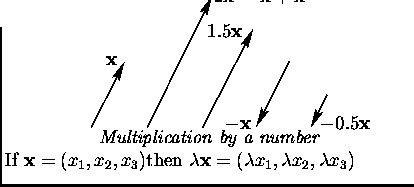
Vectors, operations on vectors, coordinates.


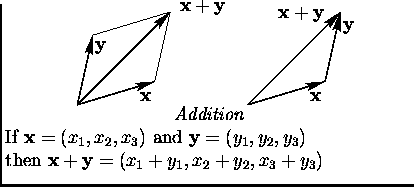
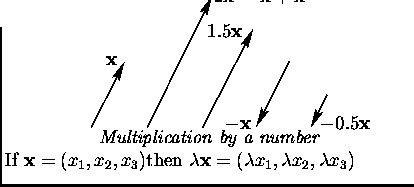
$\textstyle \parbox{9cm}{\begin{displaymath} \mbox{\begin{picture} (60,60)(0,0) ... ...(y_1,y_2,y_3)$\ \\ then $\mbox{\bf x}+\mbox{\bf y}=(x_1+y_1,x_2+y_2,x_3+y_3)$}$ $\textstyle \parbox{9cm}{\begin{displaymath} \mbox{\begin{picture} (150,60)(0,0)... ...x_2,x_3)$then ${\lambda}\mbox{\bf x}=({\lambda}x_1,{\lambda}x_2,{\lambda}x_3)$}$



An n-dimensional vector space ${\mathbb R}^n$ is the set of all ordered n-tuples of real numbers:

\begin{displaymath}{\mathbb R}^n=\{\mbox{\bf x}=(x_1,\dots,x_n) \vert x_i\in{\mathbb R}\}\ .\end{displaymath}

If $\mbox{\bf x}=(x_1,\dots,x_n)$ and $\mbox{\bf y}=(y_1,\dots,y_n)$ then $\mbox{\bf x}+\mbox{\bf y}=(x_1+y_1,\dots,x_n+y_n)$ and ${\lambda}\mbox{\bf x}=({\lambda}x_1,\dots,{\lambda}x_n)$.

Obvious properties of the operations.         $\begin{array}[t]{rcl} (\mbox{\bf x}+\mbox{\bf y})+\mbox{\bf z}&=&\mbox{\bf x}+(... ... x}+\mbox{\bf0}&=&\mbox{\bf x}\\ 0\cdot \mbox{\bf x}&=&\mbox{\bf0} \end{array}$





Linear combination ${\lambda}_1\mbox{\bf v}_1+{\lambda}_2\mbox{\bf v}_2+\dots+{\lambda}_n\mbox{\bf v}_n$.
In particular $\mbox{\bf x}=(x_1,\dots,x_n)=x_1\mbox{\bf e}_1+x_2\mbox{\bf e}_2+\dots+x_n\mbox{\bf e}_n$, where $\mbox{\bf e}_1=(1,0,0\dots,0)$; $\mbox{\bf e}_2=(0,1,0\dots,0)$; $\mbox{\bf e}_3=(0,0,1\dots,0)$; ...; $\mbox{\bf e}_n=(0,0,0\dots,1)$.





Linear independence.
Definition. Vectors $\mbox{\bf v}_1$, $\mbox{\bf v}_2$, ..., $\mbox{\bf v}_r$ are said to be linearly dependent if the zero vector $\mbox{\bf0}=(0,\dots, 0)$ is a nontrivial linear combination of $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_r$. This means, there exist r numbers ${\lambda}_1$,..., ${\lambda}_r$ not all zero such that ${\lambda}_1\mbox{\bf v}_1+ \dots+ {\lambda}_r\mbox{\bf v}_r=\mbox{\bf0}$.
If the vectors are not linearly dependent, they are said to be linearly independent.

Proposition. If $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_r$ are linearly dependent then vectors $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_r$, $\mbox{\bf v}_{r+1}$, ..., $\mbox{\bf v}_l$ is also linearly dependent for arbitrary vectors $\mbox{\bf v}_{r+1}$, ..., $\mbox{\bf v}_l$.

Theorem. Suppose r>n. Then any r vectors $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_r$ in ${\mathbb R}^n$ are linearly dependent.

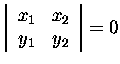Example. Vectors $\mbox{\bf x}=(x_1,x_2)$ and $\mbox{\bf y}=(y_1,y_2)$ are linearly dependent if and only if $\left\vert\begin{array}{cc} x_1&x_2\\ y_1&y_2 \end{array}\right\vert=0$.





Basis.
Definition. A set of vectors $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_n$ is called a basis of the space ${\mathbb R}^n$ if for every $\mbox{\bf x}\in{\mathbb R}^n$ there is a unique linear combination of $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_n$ which is equal to $\mbox{\bf x}$.

Theorem. Any set of n linearly independent vectors in ${\mathbb R}^n$ is a basis of ${\mathbb R}^n$.

Theorem. Suppose $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_r$ are linearly independent vectors in ${\mathbb R}^n$ and r<n. Then there exist vectors $\mbox{\bf v}_{r+1}$, ..., $\mbox{\bf v}_n$ such that the set { $\mbox{\bf v}_1$, ..., $\mbox{\bf v}_r$, $\mbox{\bf v}_{r+1}$, ..., $\mbox{\bf v}_n$} is a basis of ${\mathbb R}^n$.