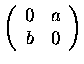LINEAR ALGEBRA (Math 211)
HW #11 (Due Mon. Nov. 6 )


1. Determine which sets are vector spaces under the given operations. For those which are not, explain why.

(a) the set of triangular matrices with the usual addition and scalar multiplication;

(b) the set of matrices having the form 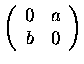$\left(\begin{array}{cc} 0&a\\ b&0 \end{array}\right)$ with the usual addition and scalar multiplication;

(c) the set of polynomials of degree $\leq4$ ( ax4+bx3+cx2+dx+e) with the usual operations;

(d) the set of polynomials of degree $\leq4$ with the highest coefficient 1 ( x4+ax3+bx2+cx+d) and
the usual operations;

(e) the set of all pairs of real numbers (x,y) with the operations

\begin{displaymath}(x,y)+(x',y')=(x+x', y+y'-1)\qquad\mbox{and}\qquad {\lambda}(x,y)=({\lambda}x,{\lambda}y)\ ;\vspace{-10pt}\end{displaymath}

(f) the set of all pairs of positive real numbers (x,y) with the operations

\begin{displaymath}(x,y)+(x',y')=(xx', yy')\qquad\mbox{and}\qquad {\lambda}(x,y)=(x^{{\lambda}},y^{{\lambda}})\ ;\vspace{-10pt}\end{displaymath}


2. Determine whether or not the following vectors span ${\mathbb R}^2$.

( a)    (1,2) and (-1,1)  ( c)    (-2,1), (1,3) and (2,4)
( b)    (2,3) and (4,6)  ( d)    (-1,2), (1,-2) and (2,-4)


3. Which of the following polynomials span the vector space of polynomials of degree $\leq2$ (ax2+bx+c)

( a)    1, x2, x2-2  ( c)    x+2, x+1, x2-1
( b)    2, x2, x, 2x+3  ( d)    x+2, x2-1


4. Let $\mbox{\bf v}_1=(-1,2,3)$ and $\mbox{\bf v}_2=(3,4,2)$. Determine whether or not the following vector $\mbox{\bf x}$ belongs to $\mbox{Span}(\mbox{\bf v}_1,\mbox{\bf v}_2)$ (if ``yes" represent $\mbox{\bf x}$ as a linear combination of $\mbox{\bf v}_1$ and $\mbox{\bf v}_2$)

( a)     $\mbox{\bf x}=(2,2,6)$  ( b)     $\mbox{\bf x}=(-9,-2,5)$ .


5. Let U and V be subspaces of a vector space W. Prove that $U\cap W$ is also a subspace of W.