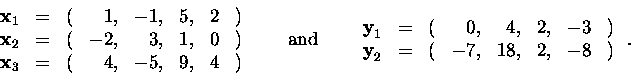LINEAR ALGEBRA (Math 211)
HW #13 (Due Wed. Nov. 15 )


1. Find the dimension of the linear space ${\cal M}(m,n)$ of all matrices with m rows and n columns.



In problems 2,3,4 find a basis and the dimension of a linear space spanned by the following vectors:


2. $\mbox{\bf v}_1=(2,1,3,1)$, $\mbox{\bf v}_2=(1,2,0,1)$, $\mbox{\bf v}_3=(-1,1,-3,0)$.


3. $\mbox{\bf v}_1=(2,0,1,3,-1)$, $\mbox{\bf v}_2=(1,1,0,-1,1)$, $\mbox{\bf v}_3=(0,-2,1,5,-3)$, $\mbox{\bf v}_4=(1,-3,2,9,-5)$


4. $\mbox{\bf v}_1=(2,1,3,-1)$, $\mbox{\bf v}_2=(-1,1,-3,1)$, $\mbox{\bf v}_3=(4,5,3,-1)$, $\mbox{\bf v}_4=(1,5,-3,1)$



Find the ranks of following matrices:

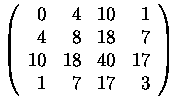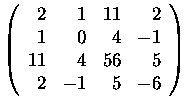5.     $\left(\begin{array}{rrrr} 0&4&10&1\\ 4&8&18&7\\ 10&18&40&17\\ 1&7&17&3 \end{array}\right)$                 6.     $\left(\begin{array}{rrrr} 2&1&11&2\\ 1&0&4&-1\\ 11&4&56&5\\ 2&-1&5&-6 \end{array}\right)$                 7.     $\left(\begin{array}{rrrr} 2&1&1&1\\ 1&3&1&1\\ 1&1&4&1\\ 1&1&1&5\\ 1&2&3&4\\ 1&1&1&1 \end{array}\right)$        


Find the general solutions of the following systems:


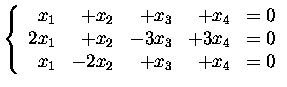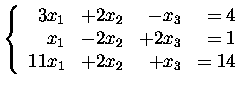
8.     $\displaystyle\left\{\begin{array}{rrrrr} x_1& +x_2& +x_3& +x_4&=0\\ 2x_1& +x_2&-3x_3&+3x_4&=0\\ x_1&-2x_2& +x_3& +x_4&=0 \end{array}\right.$                 9.     $\displaystyle\left\{\begin{array}{rrrr} 3x_1&+2x_2& -x_3&=4\\ x_1&-2x_2&+2x_3&=1\\ 11x_1&+2x_2& +x_3&=14 \end{array}\right.$



10. Find the dimension and a basis of the intersection $\mbox{Span}(\mbox{\bf x}_1, \mbox{\bf x}_2, \mbox{\bf x}_3)\cap \mbox{Span}(\mbox{\bf y}_1, \mbox{\bf y}_2)$, where

\begin{displaymath}\begin{array}{ccrrrrrl} \mbox{\bf x}_1&=&(&1,&-1,&5,&2&) \\ ... ...,&2,&-3&) \\ \mbox{\bf y}_2&=&(&-7,&18,&2,&-8&) \end{array}\ .\end{displaymath}