LINEAR ALGEBRA (Math 211)
HW #15 (Due Fri. Dec. 1 )


1. Find the transition matrix from the basis ${\cal B}$ to the basis ${\cal B}'$

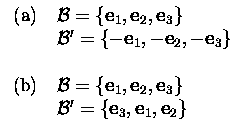
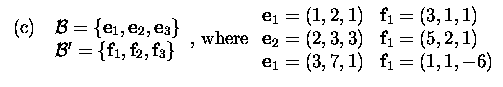
$\textstyle \parbox{5.3cm}{ \begin{tabular}{cl} (a)&${\cal B}=\{\mbox{\bf e}_1,\... ...\ &${\cal B}'=\{\mbox{\bf e}_3,\mbox{\bf e}_1,\mbox{\bf e}_2\}$\end{tabular}}$                 $\textstyle \parbox{11cm}{ \begin{tabular}{cl} (c)&${\cal B}=\{\mbox{\bf e}_1,\m... ...(5, 2, 1)\\ \mbox{\bf e}_1=(3, 7, 1) & \mbox{\bf f}_1=(1, 1, -6) \end{array}$}$


2. Let A and B be two linear operators on ${\mathbb R}^3$ given by the formulas
A(x,y,z)=(2x,-2x+3y+2z,4x-y+5z)
B(x,y,z)=(-3x+z,2y+z,-y+3z).

Put $C=A\circ B - B\circ A$. Find the matrices of A, B, and C with respect to the standard basis.


3. The standard basis for the linear space of 2 x 2 matrices ${\cal M}(2,2)$ consists of four matrices

\begin{displaymath}\left(\begin{array}{cc}1&0\\ 0&0\end{array}\right)\ ,\qquad\q... ...ad\qquad \left(\begin{array}{cc}0&0\\ 0&1\end{array}\right)\ .\end{displaymath}

Write the matrix of a linear operator $T:{\cal M}(2,2)\to {\cal M}(2,2)$ given by the formula T(A)=AT with respect to this basis.


4. A linear operator $T:{\mathbb R}^4\to{\mathbb R}^4$ has a matrix $\left(\begin{array}{cccc} 1&2&0&1\\ 3&0&-1&2\\ 2&5&3&1\\ 1&2&1&3\\ \end{array}\right)$ with respect to the standard basis ${\cal B}=\{\mbox{\bf e}_1,\mbox{\bf e}_2,\mbox{\bf e}_3,\mbox{\bf e}_4\}$. Find the matrices of this operator with respect to the bases

(a)     ${\cal B}'=\{\mbox{\bf e}_1,\mbox{\bf e}_3,\mbox{\bf e}_2,\mbox{\bf e}_4\}$                          (b)     ${\cal B}'=\{\mbox{\bf e}_1,\mbox{\bf e}_1+\mbox{\bf e}_2,\mbox{\bf e}_1+\mbox{\... ...+\mbox{\bf e}_3, \mbox{\bf e}_1+\mbox{\bf e}_2+\mbox{\bf e}_3+\mbox{\bf e}_4\}$


5. Prove that the composition of two rotations by angles ${\alpha}$ and ${\beta}$ in ${\mathbb R}^2$ is the rotation by the angle ${\alpha}+{\beta}$.