Sheet #7

LINEAR ALGEBRA (Math 211)
Sheet #7
LINEAR TRANSFORMATIONS

A linear transformation is a map $T: V\to W$ from the vector space V into the vector space W satisfying two conditions.
$\fbox{$T(\mbox{\bf x}+ \mbox{\bf y}) = T(\mbox{\bf x}) + T(\mbox{\bf y})$}$ , and

$\fbox{$T({\lambda}\mbox{\bf x})={\lambda}T(\mbox{\bf x})$}$ for any $\mbox{\bf x}$ , $\mbox{\bf y}$ from V and any ${\lambda}$ from ${\mathbb R}$ .

Examples. V=W=P_n is the space of polynomials of degree $\leq n$ .
(1) $T={d\over dx}$ . (2)Sifting operator: $T:f(t)\mapsto f(t+1)$ .

Matrix of a linear transformation T. Let $\mbox{\bf e}_1$ , $\mbox{\bf e}_2$ , ..., $\mbox{\bf e}_n$ be a basis for V and $\mbox{\bf f}_1$ , $\mbox{\bf f}_2$ , ..., $\mbox{\bf f}_m$ be a basis for W. If

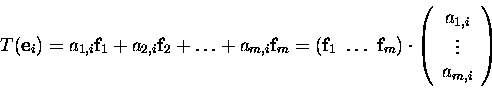
$\begin{displaymath}T(\mbox{\bf e}_i)= a_{1,i}\mbox{\bf f}_1 + a_{2,i}\mbox{\bf f... ...t(\begin{array}{c}a_{1,i}\\ \vdots\\ a_{m,i}\end{array}\right) \end{displaymath}$

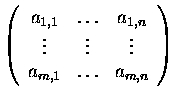then the matrix A_T= $\left( \begin{array}{ccc} a_{1,1}&\dots&a_{1,n}\\ \vdots&\vdots&\vdots\\ a_{m,1}&\dots&a_{m,n}\end{array}\right)$ is called the matrix of the linear transformation T with respect to the chosen bases $\mbox{\bf e}_1$ , ..., $\mbox{\bf e}_n$ for V and $\mbox{\bf f}_1$ , ..., $\mbox{\bf f}_m$ for W.

Theorem. For a vector $\mbox{\bf x}= x_1\mbox{\bf e}_1 + x_2\mbox{\bf e}_2+\dots+ x_n\mbox{\bf e}_n$ from V the coordinates of the vector $\mbox{\bf y}=T(\mbox{\bf x})$ with respect to the basis $\mbox{\bf f}_1$ , ..., $\mbox{\bf f}_m$ can be written as

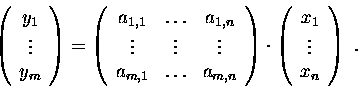
$\begin{displaymath}\left(\begin{array}{c}y_1\\ \vdots\\ y_m\end{array}\right) = ... ...t \left(\begin{array}{c}x_1\\ \vdots\\ x_n\end{array}\right)\ .\end{displaymath}$

Composition of linear transformations. Let $T: V\to W$ and $L: W\to U$ be linear transformations. Their composition $L\circ T$ is a linear transformation from V to U such that $(L\circ T)(\mbox{\bf x})=L\left(T(\mbox{\bf x})\right)$ . Then $\fbox{$A_{L\circ T} = A_L\cdot A_T$}$ , where

A_L is the matrix of L with respect to the bases $\mbox{\bf e}_1$ ,..., $\mbox{\bf e}_n$ for V and $\mbox{\bf f}_1$ , ..., $\mbox{\bf f}_m$ for W;

A_T is the matrix of L with respect to the bases $\mbox{\bf f}_1$ ,..., $\mbox{\bf f}_m$ for W and $\mbox{\bf g}_1$ , ..., $\mbox{\bf g}_k$ for U;

$A_{L\circ T}$ is the matrix of $L\circ T$ with respect to the bases $\mbox{\bf e}_1$ ,..., $\mbox{\bf e}_n$ for V and $\mbox{\bf g}_1$ , ..., $\mbox{\bf g}_k$ for U.

Transition matrix P from an old basis ${\cal B}$ to a new one ${\cal B}'$ .

$\textstyle \parbox{8cm}{For vectors:\quad $\left(\mbox{\bf e}'_1\ \dots\ \mbox{\bf e}'_n\right)= \left(\mbox{\bf e}_1\ \dots\ \mbox{\bf e}_n\right)\cdot P$}$ $\textstyle \parbox{8cm}{For coordinates:\quad{ $\left(\begin{array}{c}x_1\\ \vd... ...}= $P\cdot${ $\left(\begin{array}{c}x'_1\\ \vdots\\ x'_n\end{array}\right)$}}$

Theorem. Let A_T be the matrix of the linear transformation $T: V\to W$ with respect to the bases $\mbox{\bf e}_1$ ,..., $\mbox{\bf e}_n$ for V and $\mbox{\bf f}_1$ , ..., $\mbox{\bf f}_m$ for W. Then

$A'_T = P^{-1}_W\cdot A_T\cdot P_V$

is the matrix of T with respect to the new bases $\mbox{\bf e}'_1$ ,..., $\mbox{\bf e}'_n$ for V and $\mbox{\bf f}'_1$ , ..., $\mbox{\bf f}'_m$ for W, where
P_V is the transition matrix from the basis $\mbox{\bf e}_1$ ,..., $\mbox{\bf e}_n$ to the basis $\mbox{\bf e}'_1$ ,..., $\mbox{\bf e}'_n$ and
P_W is the transition matrix from the basis $\mbox{\bf f}_1$ ,..., $\mbox{\bf f}_m$ to the basis $\mbox{\bf f}'_1$ ,..., $\mbox{\bf f}'_m$ .

A_L	is the matrix of L with respect to the bases $\mbox{\bf e}_1$ ,..., $\mbox{\bf e}_n$ for V and $\mbox{\bf f}_1$ , ..., $\mbox{\bf f}_m$ for W;
A_T	is the matrix of L with respect to the bases $\mbox{\bf f}_1$ ,..., $\mbox{\bf f}_m$ for W and $\mbox{\bf g}_1$ , ..., $\mbox{\bf g}_k$ for U;
$A_{L\circ T}$	is the matrix of $L\circ T$ with respect to the bases $\mbox{\bf e}_1$ ,..., $\mbox{\bf e}_n$ for V and $\mbox{\bf g}_1$ , ..., $\mbox{\bf g}_k$ for U.