LINEAR ALGEBRA (Math 211)
HW #17 (Due Wed. Dec. 6 )


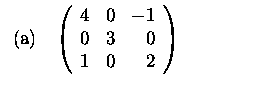
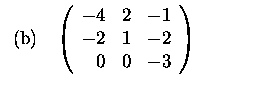
1. Find the dimensions and bases for all eigenspaces of the following operators

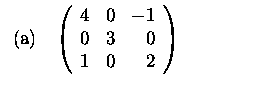
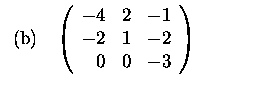
$\textstyle \parbox{6cm}{ \begin{tabular}{cl} (a)&$\left(\begin{array}{rrr} 4&0&-1\\ 0&3&0\\ 1&0&2 \end{array}\right)$\end{tabular}}$                 $\textstyle \parbox{6cm}{ \begin{tabular}{cl} (b)&$\left(\begin{array}{rrr} -4&2&-1\\ -2&1&-2\\ 0&0&-3 \end{array}\right)$\end{tabular}}$



The purpose of the following problems 2-6 is to derive a closed formula for Fibonacci numbers Fn (F0=1, F1=1, Fn= Fn-1+Fn-2 for all integers n>2). The ``closed formula" means not a recurrent formula as above which expresses Fn in terms of previous numbers, but rather a formula which expresses Fn in terms of n only.


2. Prove that

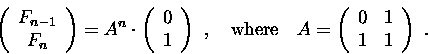
\begin{displaymath}\left(\begin{array}{c}F_{n-1}\\ F_n\end{array}\right) = A^n\c... ...e}\quad A=\left(\begin{array}{cc}0&1\\ 1&1\end{array}\right)\ .\end{displaymath}


3. Suppose that the matrices A and B are similar. So there exist an invertible matrix P such that $A=P^{-1}\cdot B\cdot P$. Prove that $A^n=P^{-1}\cdot B^n\cdot P$ for any integer n.


4. Diagonalize the matrix 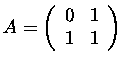$A=\left(\begin{array}{cc}0&1\\ 1&1\end{array}\right)$ from the problem 2. This means find an invertible matrix P and a diagonal matrix B such that $A=P^{-1}\cdot B\cdot P$.


5. (a) Find the matrix Bn for B from the previous problem.

     (b) Using the problem 3 find An for A from the previous problem.


6. Find the closed formula for Fibonacci number Fn.