LINEAR ALGEBRA (Math 211)
Sheet #8
LINEAR TRANSFORMATIONS 2

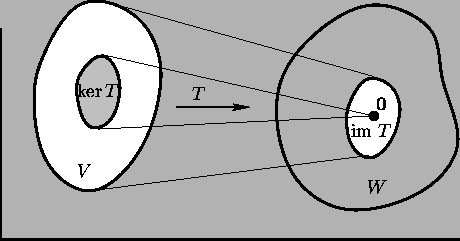
Kernel and image of a linear transformation $T: V\to W$:

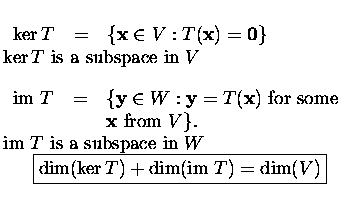
$\textstyle \parbox{7.8cm}{ \par \bigskip \begin{tabular}{rcl} $\ker T $&$=$&$\{... ...displaymath}\fbox{$\dim(\ker T)+\dim(\mbox{im\ } T)=\dim(V)$}\end{displaymath}}$         $\textstyle \parbox{10cm}{\begin{displaymath} \mbox{\begin{picture} (270,120)(0,... ...(220,20){\mbox{$W$}} \put(110,78){\mbox{$T$}} \end{picture}}\end{displaymath}}$

Choice of bases $\mbox{\bf e}_1$, $\mbox{\bf e}_2$, ..., $\mbox{\bf e}_n$ for V and $\mbox{\bf f}_1$, $\mbox{\bf f}_2$, ..., $\mbox{\bf f}_m$ for W gives the isomorphisms (identifications) V with ${\mathbb R}^n$ and W with ${\mathbb R}^m$. In this case the kernel and the image of the linear transformation T coincide with the kernel and the image of the matrix AT (see sheet #6) with respect to the chosen bases.



Theorem. Suppose AT is the matrix of a linear operator $T:V\to V$ with respect to some basis for V. Then the characteristic polynomial (see sheet ) $\det(A_T-{\lambda}I)$ depends only on the operator T and does not depend on the choice of basis for V.

Proof. A change of basis for V changes the matrix of the operator T as follows $A'_T = P^{-1}\cdot A_T\cdot P$. Then

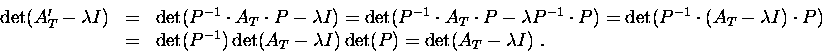
\begin{displaymath}\begin{array}{rcl} \det(A'_T-{\lambda}I) &=& \det(P^{-1}\cdot... ...t(A_T-{\lambda}I) \det(P) = \det(A_T-{\lambda}I)\ . \end{array}\end{displaymath}

Corollary. Eigenvalues of the matrix AT (the roots of the characteristic polynomial (see sheet ) do not depend on the choice of basis for V. So they are invariants of the operator T.



Definition. An eigenvector corresponding to an eigenvalue ${\lambda}$ of a linear operator T is a vector $\mbox{\bf x}\in V$ such that $T(\mbox{\bf x})={\lambda}\mbox{\bf x}$.

Definition. All eigenvectors corresponding to a given eigenvalue ${\lambda}$ form a subspace of V which is called eigenspace corresponding to ${\lambda}$.

Theorem. Eigenvectors corresponding to distinct eigenvalues are linearly independent.



Diagonalization. A linear operator $T:V\to V$ is diagonalizable if there is a basis for V with respect to which the matrix of T is diagonal.


Suppose AT is a matrix of T with respect to some basis. Then T is diagonalizable if there is an invertible matrix P such that $P^{-1}\cdot A_T\cdot P$ is a diagonal matrix.


If T has n distinct real eigenvalues, where $n=\dim(V)$. Then T is diagonalizable and the basis with respect to which T has a diagonal matrix consists of the n eigenvectors.