Mount Holyoke College
Math 200: Calculus IIA
Instructor: Sergei Chmutov
- Office: Clapp 423
- Telephone x2720
- email: schmutov
- Office hours: Tuesday, Thursday 6:00-8:00 pm or by appointment
Lectures: Tuesday, Thursday 10:50-12:05 and Friday 12:00-12:50 in
Clapp 402.
Textbook: Hughes-Hallett, Gleason, et al.,
"Calculus. Single variable". Second edition.
1998 John Wiley & Sons, Inc.
Tests: There will be five tests on each chapter from 6 to 10 of the
textbook and a self-scheduled final examination.
Grading: Each test gives 100 pt, homeworks (all together) give 100
pt, final exam gives 200 pt.
Graders: Oksana M Nagayets (omnagaye) and Marina Kolomiets
(mpkolomi)
List of students
Syllabus
Class 1 (Jan. 28. Thursday, 9:25-10:40)
Antiderivatives. Notion and formulas for simplest functions. (Sec.6.2,
page 298)
Homework #1 (due Feb.4, Thursday) Sec.6.2, page 302:
4,9,12,18,27,38,54.
Class 2 (Jan. 29. Friday, 12:00-12:50)
Simple differential equations. (Sec. 6.3, page 304)
Homework #2 (due Feb.5, Friday) Sec.6.3, page 307:
2,3,5,6,10
Class 3 (Feb. 2. Tuesday, 9:25-10:40)
Second Fundamental Theorem of Calculus. Definite integrals with a variable
as the upper limit. (Sec. 6.4, page 309)
Homework #3 (due Feb.9, Tuesday) Sec.6.4, page 312:
8,9,11,14,17
Class 4 (Feb. 4. Thursday, 9:25-10:40)
Integration by substitution. (Sec. 7.1, page 322)
Homework #4 (due Feb.11, Thursday) Sec.7.1, page 326:
11,15,16,26,33
Class 5 (Feb. 5. Friday, 12:00-12:50)
Review for test #1 on Chapter 6.
No homework
Class 6 (Feb. 9. Tuesday, 9:25-10:40)
Class 7 (Feb. 11. Thursday, 9:25-10:40)
Integration by substitution. (Sec. 7.2, page 328)
Homework #5 (due Feb.18, Thursday) Sec.7.2, page 331:
2,4,8,15,23
Class 8 (Feb. 12. Friday, 12:00-12:50)
Integration by parts. (Sec. 7.3, page 333)
Homework #6 (due Feb.19, Friday) Sec.7.3, page 337:
2,10,24,31,33
Class 9 (Feb. 16. Tuesday, 9:25-10:40)
Practice on integration. (Sec. 7.4, page 339)
Homework #7 (due Mar.2, Tuesday) Sec.7.4, page 343:
1--32, except 9,13,18,23,26,29,30,32
Class 10 (Feb. 18. Thursday, 9:25-10:40)
Approximations of definite integrals. (Sec. 7.5, page 344 and Sec.7.6,
page 350)
Homework #8 (due Feb.25, Thursday) Sec.7.5, page 348:
1,2,4,5(use n=8 instead n=32)
Class 11 (Feb. 19. Friday, 12:00-12:50)
Improper integrals. (Sec. 7.7, page 356)
Homework #9 (due Feb.26, Friday) Sec.7.7, page 363:
1,8,14,17,25
Class 12 (Feb. 23. Tuesday, 9:25-10:40)
Improper integrals. (Sec. 7.8, page 364)
Homework #10 (due Mar.2, Tuesday) Sec.7.8, page 367:
1,7,8,9,16
Class 13 (Feb. 25. Thursday, 9:25-10:40)
Applications of integrals to geometry. (Sec. 8.1, page 376)
Homework #11 (due Mar.5, Friday) Sec.8.1, page 382:
3,7,8,19,20
Bonus Problem (20 points):
Find the indefinite integral 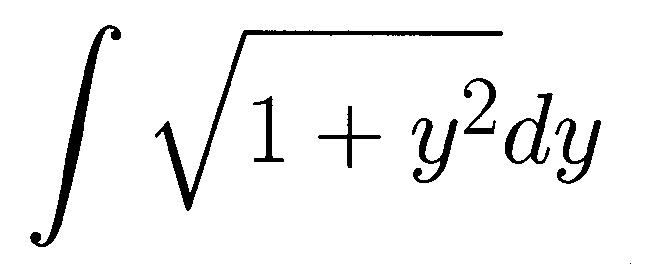 .
.
(Caution: It is not allowed to use formulas from the inside back
cover of the textbook.)
Class 14 (Feb. 26. Friday, 12:00-12:50)
Review for test #2 on Chapter 7.
No homework
Class 15 (Mar. 2. Tuesday, 9:25-10:40)
Review for test #2 on Chapter 7.
No homework
Class 16 (Mar.4. Thursday, 9:25-10:40)
Class 17 (Mar. 5. Friday, 12:00-12:50)
Applications of integrals to physics. (Sec. 8.2, page 384 and Sec. 8.3,
page 390)
Homework #13 (due Mar.12, Friday) Sec.8.2, page 388:
1b, 1c --- Find the center of mass.
Sec.8.3, page 396:
9,10
Class 18 (Mar. 9. Tuesday, 9:25-10:40)
Applications of integrals to economics. (Sec. 8.4, page 398)
Homework #14 (due Mar.23, Tuesday) Sec.8.4, page 403:
4,11
Class 19 (Mar.11. Thursday, 9:25-10:40)
Parametrized curves. (Appendix F, page 604 and Appendix G, page 610)
No homework
Bonus Problem:
Class 20 (Mar. 12. Friday, 12:00-12:50)
Complex numbers. (Appendix D, page 595)
No homework
Mar. 16, 18, 19 --- Spring break
Class 21 (Mar. 23. Tuesday, 9:25-10:40)
Functions in complex variable. (Appendix D, page 595)
No homework
Class 22 (Mar.25. Thursday, 9:25-10:40)
Taylor series. (Sec. 9.1, page 426)
Homework #15 (due Apr.1, Thursday) Sec.9.1, page 434:
3,8,11,14,31
Class 23 (Mar. 26. Friday, 12:00-12:50)
Review for test #3 on Chapter 8.
No homework
Class 24 (Mar. 30. Tuesday, 9:25-10:40)
Class 25 (Apr. 1. Thursday, 9:25-10:40)
Taylor series. (Sec. 9.1, page 426)
Homework #16 (due Apr.8, Thursday) Sec.9.1, page 434:
16,19,24,26,28
Class 26 (Apr. 2. Friday, 12:00-12:50)
Series. Convergency (Sec. 9.2, page 435)
Homework #17 (due Apr.9, Friday) Sec.9.2, page 444:
16,27,29,31, Find the Taylor expansion of the function
(1+x)a near x=0.
Class 27 (Apr. 6. Tuesday, 9:25-10:40)
Fourier series. (Sec. 9.5, page 458)
Homework #18 (due Apr.13, Tuesday) Sec.9.5, page 468:
6,8,21a,21b.
ASSIGNMENT IS CANCELLED
Class 28 (Apr. 8. Thursday, 9:25-10:40)
Differential equations. Basic notions (Sec. 10.1, page 490).
Slope fields (Sec. 10.2, page 494).
Homework #19 (due Apr.15, Thursday) Sec.10.1, page 494:
9,10; Sec.10.2, page 499:
3,5
Class 29 (Apr. 9. Friday, 12:00-12:50)
Review for test #4 on Chapter 9.
No homework
Class 30 (Apr. 13. Tuesday, 9:25-10:40)
Class 31 (Apr.15. Thursday, 9:25-10:40)
Separation of variables. (Sec. 10.4, page 505)
Homework #20 (due Apr.22, Tuesday) Sec.10.4, page 509:
1,2,6,14,18
Class 32 (Apr. 16. Friday, 12:00-12:50)
Separation of variables. (Sec. 10.4, page 505)
Homework #21 (due Apr.23, Tuesday) Sec.10.4, page 509:
13,20,22,31,32
Class 33 (Apr. 20. Tuesday, 9:25-10:40)
Second-order differential equations. (Sec. 10.8, page 542)
Homework #22 (due Apr.27, Tuesday) Sec.10.8, page 548:
3,8a,8b
Class 34 (Apr. 22. Thursday, 9:25-10:40)
Linear second-order ODEs with constant coefficients. (Sec. 10.9, page
550)
Homework #23 (due Apr.29, Thursday) Sec.10.9, page 556:
2,10,14,16,18
Class 35 (Apr. 23. Friday, 12:00-12:50)
Review for test #5 on Chapter 10.
No homework
Class 36 (Apr. 27. Tuesday, 9:25-10:40)
Class 37 (Apr.29. Thursday, 9:25-10:40)
Solutions of the bonus problems.
No homework
Class 38 (Apr. 30. Friday, 12:00-12:50)
Solutions of problems.
No homework
Class 39 (May. 4. Tuesday, 9:25-10:40)
Last day of classes
Review for the final examination
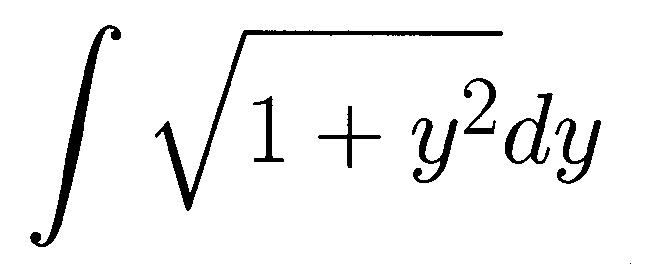 .
.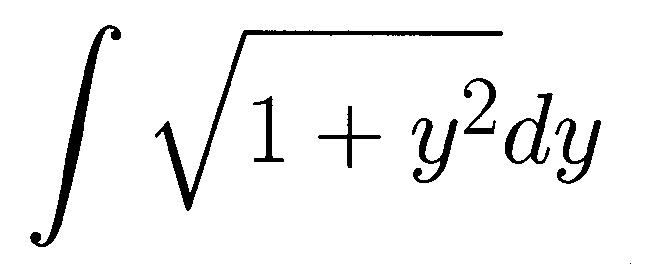 .
.![[hyperbola]](hyperbola.jpg)