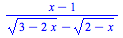Write-ups of
the problems below
are due Monday Oct. 16
Monday
Oct 9
Topics:
A.3: Theorem 4 (no proof), Theorem 3 (deduced from Theorem 4),
and 5 (with proof).
Solve,
write up and turn in: Sec. 2.6 (p. 80) 30, 34, 36,37,39 and
Calculate the following limits as x->0:
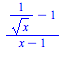 and
and 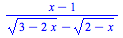
Tuesday
Oct 10
Topics: Differentiability
and the definition of the derivative Sec.2.3
Solve,
write up and turn in: Note: in the first limit above take
either x->0+ or x->1.
and explain why the problem as given is incorrectly formulated.
Sec. 2.3 (p. 62) Use the
definition of the derivative to calculate
the derivatives in the following 4, 7, 11, 24, 32, 38
1. Show that the function f(x)=|x|
is not differentiable at x=0.
2. Is the function g(x)=x|x|
differentiable at x=0?
Wednesday
Oct 11
Topics: tangent
line Sec. 2.2, Calculation of derivatives 3.1
Solve: Sec. 2.2 (p.57) 1, 11
Solve,
write up and turn in: Sec.
2.2 (p.57) 2, 7, 8 (Note that the derivatives need to be calculated
using the definition,
exccept for c,x,x^2,...x^n)
and
3. Deduce the formula a^n-b^n
= (a-b) (a^(n-1) + a^(n-2)b
+...+ ab^(n-2) + b^(n-1))
by replacing r=b/a in the formula 1-r^n
= (1-r) (1+ r +...+ r^(n-2)
+ r^(n-1))
4. Prove that the
derivative of x^n is nx^(n-1) Hint: use the above factorization.
Thursday
Oct 12
Topics: 3.1,
3.2
Solve: Sec. 3.1, 3.2
solve as many problems as needed to ensure you master the calculation
of derivatives.
Here
are a few suggestions. Sec. 3.1 - 1a,b,f , 7, 9
Sec. 3.2 - 1, 8, 9, 11, 13, 23, 29, 31
Solve,
write up and turn in: Sec.
3.1 (p.87) 6, 10, 11, 14, 15, 17, 22, 23
Sec. 3.2 (p. 92) 38, 44, 46
If you erred on the first problem of
the quiz on Wednesday:
practice the trick of amplifying the fraction with the "conjugate" sum
of radical in the following problem.
Use the definition of the derivative to calculate the derivatives of
the functions
f(x)=square root of x (see the solution in
Sec. 2.3 Example 3, p. 60), g(x)= square root of (x+2).
Friday
Oct 13
Topics: 3.3
Solve: Sec. 3.3
solve as many problems as needed to ensure you master the calculation
of derivatives.
Here
are a few suggestions. Sec. 3.3- 1, 3, 5,7, 11, 13, 33, 35
Solve,
write up and turn in: Sec.
3.3- 43, 45b,c, 46 (in problem 46 also check your answer!).
Also
5.
Derive the formula for the chain rule by using the approximation:
f(x+h) ~ f(x)+h f
'(x) .
(What you have to do is follow the calculations we did in class, erase
o(1) and replace therefore the equality sign "="
with the approximately equal sign "~")
Motivation: a very important
skill to develop for applications is working approximately.
Review the basic formulas of
trigonometry.
Bonus problem. Show (for extra 5 points!) that
if a function f(x) is continuous
and has a right derivative at a, and a left derivative at a, and the derivatives are equal,
then the function is differentiable at a.
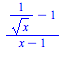 and
and