Homework due 04_03  04_10  04_18 04_24 05_01 05_08 05_16
05_22

Tutoring for H263 is held in Cockins Hall, Room 137:
Monday        3:30 – 4:30
Tuesday       11:30 – 3:30
Wednesday   11:30 – 12:30
Thursday        11:30 – 3:30

Final exam: Mon, June 5    9:30 AM - 11:18 AM (see the schedule)


Solving all the homework problems is due every day after class.


The write-ups are due Wednesday May 31.
Five problems will be graded (2 points each).


  Tuesday May 23
Solve, write up and turn in:
Find dA on a sphere radius a using a parametrization inspired by spherical coordinates
and using the formula dA= | Ru X Rv | du dv.
21.4: 15 (find the flux through direct calculation)

Solve (do not turn in): Example 4 p. 777: calculate the flux using a surface integral.

Wednesday May 24
Solve, write up and turn in:
21.4: 1a,e 3, 5, 7, 9, 13

Thursday May 25
Solve, write up and turn in:
21.4: 6, 8, 15 (using Gauss's theorem)
Also: Calculate the surface integral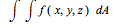 
                                                             S

of the function    f(x,y,z)=xyz   where the surface S is the triangle
with vertices A=(1,0,0), B=(0,2,0), C=(0,0,3).

Friday May 26
Solve, write up and turn in:
1. Consider the curve given parametrically by :x= cos(theta), y=sin(theta), z=theta, for 0<theta<4 Pi.
a. Show that the curve lies on the surface of the cylinder x^2+y^2=1.
b. Sketch the curve.
c. Calculate the flow of the field F=xi+yj+zk along the curve (i.e. the line integral of F. dR).
2. Find the flow of the vector field above along the segment beteen the points (1,2,3) and (0,6,0).
3. Consider a planar vector field F, which is continuously differentiable at all points in the plane.
Show that if   curl F=0 (in which case we say that F is irrotational) then the integral of f along any
closed (simple, piecewise smooth) curve in the plane is zero.

Tuesday May 30
Solve, write up and turn in:
21.5: 4, 5, 6, 7, 9

Wednesday May 31
Solve:
21.5: 1,  11
Review Chapter 21.

Final exam: Mon, June 5    9:30 AM - 11:18 AM (see the schedule)

Review guide

Formula sheet   provided with the exam.


............................................................................................................
For future reference - some formulas for dA that we have obtained:
On a cylinder radius a:  dA=a dz  d(theta)
On a sphere raius a:  dA=a^2 d(phi) d(theta).

Reference for surface area defined parametrically
Web resources: Library of Math   COW