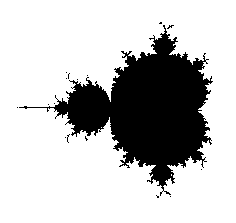
Around 1991, Dave Boll found experimentally a strange connection between pi and the Mandelbrot set. HERE is that post.
In 1992 some discussion on his questions was posted in a newsgroup. The material was then included in two books by Peitgen, Jürgens and Saupe: Chaos and Fractals (Springer-Verlag 1992) pages 859-862; and Fractals for the Classroom (Springer-Verlag 1992) Part two, pages 431-434.
There is a reference to a newsgroup post of mine, merely by the number <l992Mar27.135743.28423@zaphod.mps.ohio-state.edu>. Here it is:
Newsgroups: alt.fractals
From: edgar@function.mps.ohio-state.edu (Gerald Edgar)
Subject: Pi and the Mandelbrot set
Message-ID: <l992Mar27.135743.28423@zaphod.mps.ohio-state.edu>
Sender: usenet@zaphod.mps.ohio-state.edu
Nntp-Posting-Host: function.mps.ohio-state.edu
Organization: The Ohio State University, Dept. of Math.
Date: Fri, 27 Mar 1992 13.57.43 GMT
Lines: 73
David Petrie wrote:
] Here's a somewhat heuristic theoretical explanation of what's going on.
] atleast around the point (1/4,0).
]
] When we iterate the equation x := x^2 + 1/4+epsilon, starting at x = 0,
] x increases slowly to 1/2, and after it passes 1/2, it zooms off rapidly
] to infinity. So the interesting behavior is when x = 1/2. Let x = y+1/2.
] Then our equation reads y := y^2 + y + epsilon, or using subscripts
] y_(n+l) = (y_n)^2 + y_n + epsilon.
]
] The y_n's are increasing smoothly and slowly, atleast near y = 0, so it
] is reasonable to consider y to be a function of the continuous variable n,
] and y_(n+1) - y_n is very close to y'(n) (the derivative of y).
]
] So our equation now reads y'(n) = y^2 + epsilon. This has the solution
] y = a*tan(a*n+c) where a = Sqrt(epsilon). The intitial point and end point
] of our iteration correspond to consecutive poles of the tangent function,
] giving a*n = pi, where a = Sqrt(epsilon) and n is the number of iterations
] to leave the set, exactly what Mr. Boll has found.
]
] A similar method seems to work around the point (-3/4,0), but I haven't
] completed the analysis (it seems to require a second degree diffeq).
]
] I did a little more experimentation, and found something really neat at
] the points (-1.25,epsilon). There, n*epsilon/pi (n = #iterations) jumps
] around chaotically, but it is always very close to an integer or a half
] integer for epsilon very small. Wierd!
]
]
] David Petry
]
A reference for this approach is the Guckenheimer & Holmes book,
"Nonlinear Oscillations ...", section 6.8. I agree, it is "heuristic".
The point -3/4 can he dealt with similarly. The function f(z) = z^2-3/4
has fixed point -1/2 with eigenvalue -1. So we use f(f(z)) to get
eigenvalue +1. Transform coordinates z = -1/2 + y so that we are
interested in what happens for y near 0. Consider the
transformations z^2 - 3/4 + i*r, for small, positive, r. After some
algebra, we get the differential equation:
dy 4 3 2 2
---- = y - 2 y + 2 I r y - 2 I r y - r
dt
(Here I = sqrt(-l).) The time the trajectory spends near 0 (say between
-1 and 1) is the integral
1
/
| 1
| ---------------------------------- dy
| 4 3 2 2
/ y - 2 y +2 I r y - 2 I r y - r
-l
Its asymptotics are now shown in the articles called
"Asymptotics of an integral" in sci.math.symbolic. We conclude that
if n is the number of steps required for divergence, then
n is asymptotic to Pi/(2*r). Actually, this is the number of steps
for the composition f(f(z)), so the number of steps for f(z) itself
is double this, Pi/r. So: Mr. Boll's asymptotic behavior is vindicated.
This is a heuristic argument, so there could be some work done to make it
rigorous . . .
Now, is -5/4 the next spot to study? Or how about -2 ?
-----
|
 Maple worksheet
Maple worksheet
 plain text file
plain text file
Date: Mon, 06 Oct 1997 14:36:12 -0700 From: Jay R Hill <Jay.R.Hill@NOSPAMcpmx.saic.com> Newsgroups: sci.fractals Subject: Re: mandelbrot and pi? I took a look at several other points including -1.75. I found that there are similar relationships with different exponents on n. The trick is finding a reasonable path to follow. At -0.75 the i direction is apparent. At -1.75 a parabolic path worked, as I recall. The path has to follow nicely out through the filaments with out crossing them. The exponent depends on your parameterization of the path. Jay Hill reply to Jay.R.Hill@cpmx.saic.com |

|
The thing that really blows my mind is that this phenomenon, namely that for parabolic Julia sets, the escape rate in a neighbourhood of the landing point of a ray that goes to the Julia set at the (forward orbit of) the critical value shows up in my PhD thesis! Basically, what I show there is that there is a relation between the speed of escape of such points (in this case, polynomial in the number of iterations) and the "geometry" of the Julia set (basically what kind of 'wedges' one can stick in along landing rays). Linear wedges (in the natural coordinates) correspond to any case where there is a hyperbolic metric, corresponding to exponential escapes. When one gets to polynomial escapes, the wedges are asymptotically narrower (think x^2 around 0), which is what one observes in the parabolic and (conjecturally) in some of the Siegel cases too [ie in the exterior of the Siegel domains, the interior parts in those cases are simple]. These Julia sets (conjecturally in my thesis, but I believe that has been proven since) correspond exactly to those where the exterior conformal map extends to a Hölder continuous map on the circle