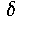 of our
previous approach.
of our
previous approach.
In this course we first give a general introduction to noncommutative
geometry. We then discuss a fundamental example of noncommutative space
related to the Riemann zeta function. This gives a spectral interpretation
of the critical zeros of the Riemann zeta function as an absorption
spectrum, while the noncritical zeros appear as resonances, and a geometric
interpretation of the explicit formulas of number theory as a trace formula
on a noncommutative space. This reduces the Riemann hypothesis to
the validity of the trace formula, which remains unproved, and eliminates
the parameter 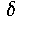 of our
previous approach.
of our
previous approach.
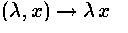 of K* on K for a local field.
of K* on K for a local field.
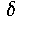 .
.
Alain Connes' expository paper on the subject matter of the course, describing his motivations and some background. It is available for downloading in any of the following formats:
This is Alain Connes' latest paper, on the subject matter of this course. It is available for downloading in any of the following formats:
The current listing for Alain Connes' course is
| MATH 975A | TOPICS IN GEOMETRY | 3 CR | Section: 18473-7 | MWF | 2:30-4:20PM | CL 0220 |
Update4: Lectures on M (Nov. 9) and F (Nov. 13) during the fifth week
The first lecture of the course will be Wed. Oct. 14. The second lecture will be Fri. Oct. 16. The lectures will be held MW the second week, WF the third week, and MW the fourth week. All lectures will be at 2:30-4:20 pm, in room CL 0220. (CL is Caldwell Laboratory, 2024 Neil Ave. Click here for a map.)