


Next: Laser-driven Particle Mechanics via
Up: Laser-driven particle mechanics
Previous: Dynamical Phase as Physical
Contents
The principle that gives rise to the above-mentioned new phase space
coordinates is the principle of constructive interference
according to which the spacetime trajectory of a particle is the locus
of events where the semi-classical wavefunction
has maximum modulus.
The mathematical formulation of this principle is based on the
evaluation of the superposition expressed by this integral whenever
the exponential phase factor is a function varying rapidly compared to
the slowly varying amplitude
 . Based on a
Gaussian weight factor
. Based on a
Gaussian weight factor 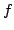 , the
superposition integral is a Gaussian also. Its maximum is located at
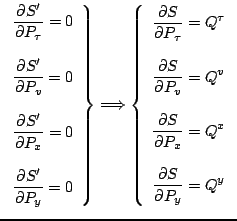
those events which satisfy
, the
superposition integral is a Gaussian also. Its maximum is located at
those events which satisfy
 |
(22) |
The left column are the conditions for constructive interference.
They comprise in Minkowski spacetime the particle's world line
as obtained from
The capitalized 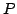 's and
's and 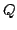 's refer to the initial value data
of the world line at
's refer to the initial value data
of the world line at
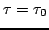 .
.
The pictorial representation of the principle of constructive
interference consists of the intersection of the isograms of two
slightly different solutions to the H-J equation. The points of
intersection are where constructive interference takes place. The
particle worldline is understood to pass through these successive
points. Figure 5 and 6
illustrate this process for free charge and and for a charge driven by
the e.m. field of a plane wave. Figure 7 illustrates it for an e.m. pulse with a finite number of
oscillations. Note that, once suitably averaged, its spacetime region
acts a refractive medium for the particle world line.
- Problem 3: a) For
Figure 7 formulate what in Euclidean
space corresponds to Snell's law.
b) Can one identify a refractive index for the laser pulse history?
If so, what is it?
Figure 5:
Constructive interference between
two sets of wave front histories, the solid isograms of
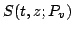 and dashed isograms of
and dashed isograms of
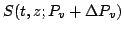 . These two sets of
wave front histories are the familiar relativistic De Broglie matter
waves. The particle is understood to be located at that event where
an isogram of one intersects with an equal-value isogram of the
other. The fact that the heavy world line and the intersecting
isograms are straight is a reflection of the fact that the charged
particle is free: there is no e.m. field.
. These two sets of
wave front histories are the familiar relativistic De Broglie matter
waves. The particle is understood to be located at that event where
an isogram of one intersects with an equal-value isogram of the
other. The fact that the heavy world line and the intersecting
isograms are straight is a reflection of the fact that the charged
particle is free: there is no e.m. field.
|
|
Figure 6:
Same as Figure 5 except that the charged particle is driven by the periodic
e.m. field of a travelling wave. In such a circumstance the
oscillating e.m. field distorts the De Broglie wave front histories so
that constructive interference results in an oscillating particle
trajectory.
|
|
Figure 7:
Relativistic De
Broglie wave front histories (solid and dashed isograms) distorted by
a three cycle laser pulse. Its spacetime history occupies the diagonal
45 swath. The constructive interference expresses the circumstance
where the particle with slight negative z-velocity passes through the
+z travelling pulse, gets jiggled three times, before it emerges with
its original velocity from the back of the pulse. The net effect of
this process is that the particle gets shifted by an amount
proportional to the duration of the pulse. If one ignores the
oscillatory effect on the De Broglie waves by averaging over each of
their histories, then the spacetime history of the laser pulse acts as
a refractive medium for the averaged particle world line.
swath. The constructive interference expresses the circumstance
where the particle with slight negative z-velocity passes through the
+z travelling pulse, gets jiggled three times, before it emerges with
its original velocity from the back of the pulse. The net effect of
this process is that the particle gets shifted by an amount
proportional to the duration of the pulse. If one ignores the
oscillatory effect on the De Broglie waves by averaging over each of
their histories, then the spacetime history of the laser pulse acts as
a refractive medium for the averaged particle world line.
|
|



Next: Laser-driven Particle Mechanics via
Up: Laser-driven particle mechanics
Previous: Dynamical Phase as Physical
Contents
Ulrich Gerlach
2005-11-07
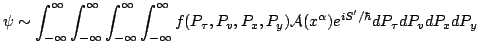
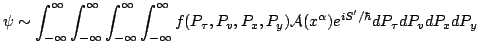
![]() . Based on a
Gaussian weight factor
. Based on a
Gaussian weight factor ![]() , the
superposition integral is a Gaussian also. Its maximum is located at
those events which satisfy
, the
superposition integral is a Gaussian also. Its maximum is located at
those events which satisfy
![\includegraphics[scale=.44]{free_particle.eps}](img153.png)
![\includegraphics[scale=.44]{driven_particle.eps}](img154.png)
![\includegraphics[scale=.6]{constr_interferInaRectPulse.eps}](img155.png)