Many from "2000 feladat az elemi matematika korebol" by Sandor Roka
Number Theory Examples.
369. [2] Prove the following divisiblity statements:
373. [2] Prove that the following numbers are all
composite.
375. [3] Prove that 49+610+320 is a composite number.
379. [4] Prove that 989*1001*1007 + 320 is a composite number.
382. [4] Prove that for any positive integer n, 19*8n
+ 17 is a composite number.
(There are typo's in the first two-- they should be >
n and > sqrt(n) ) I'll Change it asap.)
![]()

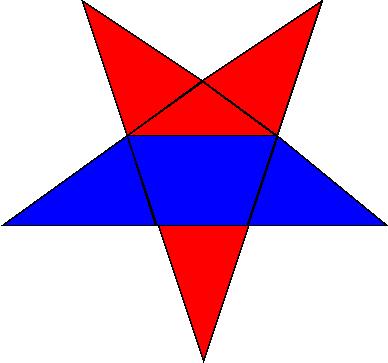
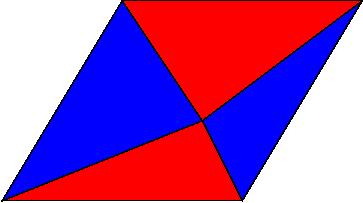
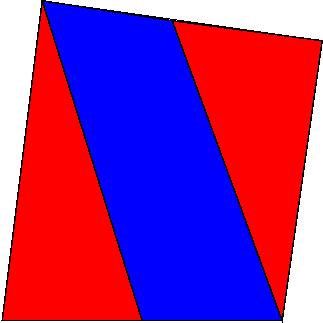
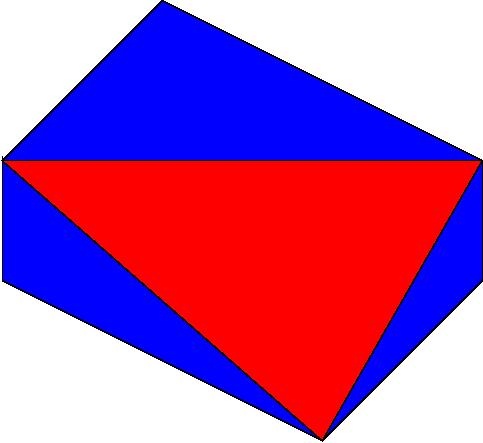
In each of the following problems prove that the area of the blue region is equal to the area of the red.
1284. [2] Connect any point in the interior of a parallelagram with the four corners.
1285. [2] Connect the midpoints of two opposite sides of a convex quadrilateral to the corners as shown.
1288. [2] In a Hexagon, with opposite sides parallel and of equal length, draw a triangle connecting alternating vertices.
1290. [2] Divide a regular star as shown.