I look forward to working with graduate students interested in the area of computational mathematics. If you are interested in learning more about what we do, please feel free to send me an email.
Brief Introduction of My Research Areas: (see the latest publications for my recent research interests)
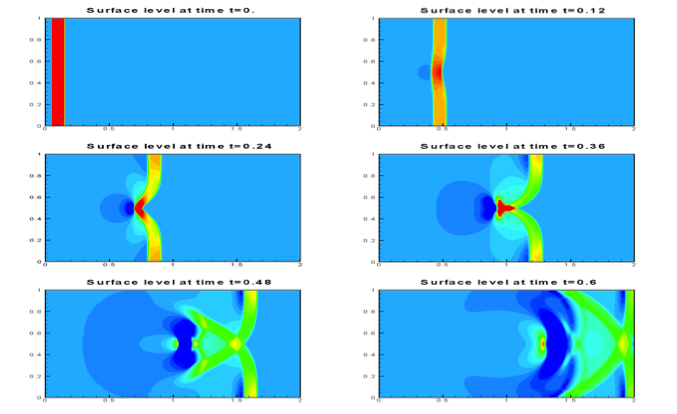
1: Shallow-water equations in storm surge modeling and coastal engineering
The shallow-water equations with a non-flat bottom topography play a critical role in modeling and simulation of the flows in rivers and coastal areas, and have wide applications in ocean, hydraulic engineering, and atmospheric modeling. This system describes the flow as a conservation law with additional source term due to the bottom topography. These equations have steady-state solutions in which the flux gradients are non-zero but exactly balanced by the source term. Therefore extra care must be paid to approximate the source term numerically. Another important difficulty arising in these simulations is the appearance of dry areas, and standard numerical methods may fail in the presence of these areas.
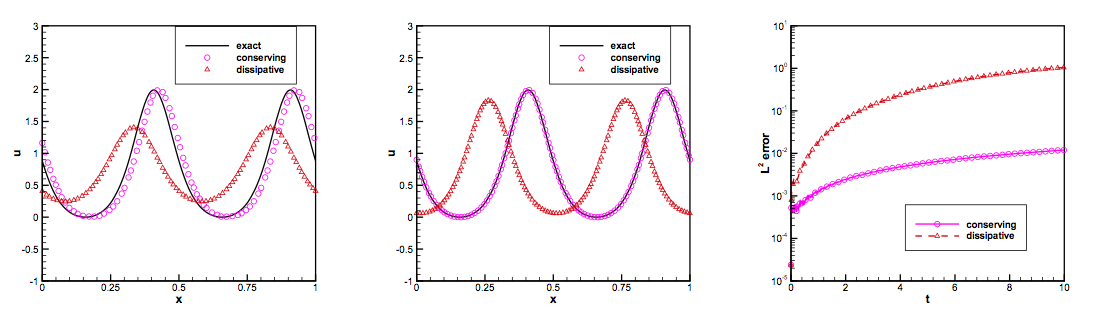
2. High-order accurate, energy conserving methods for wave propagating problems
Wave propagation problems arise in science, engineering and industry, and they are significant to geoscience, petroleum engineering, telecommunication, and the defense industry. Some wave problems have infinite many conservation laws, and usually the conservation of energy is considered due to its essential importance for long time behavior investigation.The energy conserving property is one of the guiding principles for numerical algorithms in order to provide an accurate approximation. We have developed and analyzed high order accurate, energy conserving discontinuous Galerkin methods for solving the wave equation.
3. Well-balanced methods for hyperbolic systems with source terms
Hyperbolic systems often involve source terms arising from geometrical, reactive, biological or other considerations. They have wide applications in different fields including chemistry, biology, fluid dynamics, astrophysics, and meteorology et. al. Such balance laws admit steady state solutions which are usually non-trivial and often carry important physical meaning. A straightforward numerical scheme may fail to preserve exactly these steady states. The well balanced schemes are introduced to preserve exactly some of these equilibrium solutions. One major advantage of the well balanced schemes is that they can accurately resolve small perturbations to such steady state solutions with relatively coarse meshes and promise to be efficient near steady state.
4. Efficient numerical methods for kinetic equations
5. Structure preserving methods for hyperbolic conservation laws
Research Sponsors:
Research partially supported by National Science Foundation (NSF) CAREER program, Department of Energy (DOE), Office of Naval Research (ONR) and Oak Ridge National Laboratory (ORNL), which are greatly appreciated.



