| I was grateful to recently be selected to receive a SIAM Science Policy Fellowship for 2023-2024. I am really excited to learn more about how the Science Policy arm of SIAM promotes applied and computational math at the federal government level. I'm happy to announce that I will be joining the Department of Mathematics at Trinity College in Fall 2023 as a tenure-track Assistant Professor. Thank you to everyone who helped me get here. |
| My post-doctoral work is on deep learning of dynamical systems. Here are a few projects. Please see my [CV] for more info. |
| Deep Learning of Unknown PDEs in Nodal Space [journal] [arXiv]Approximating the evolution of an infinite-dimensional function is more difficult than that of a dynamical system of ODEs. To address this, we propose a structure based on a one-step method for solving PDEs that consists of various channels modeled after partial derivative operators and a component-wise nonlinear combination to approximate the flow-map of a variety of unknown PDEs from their discretized solution data at various times. | 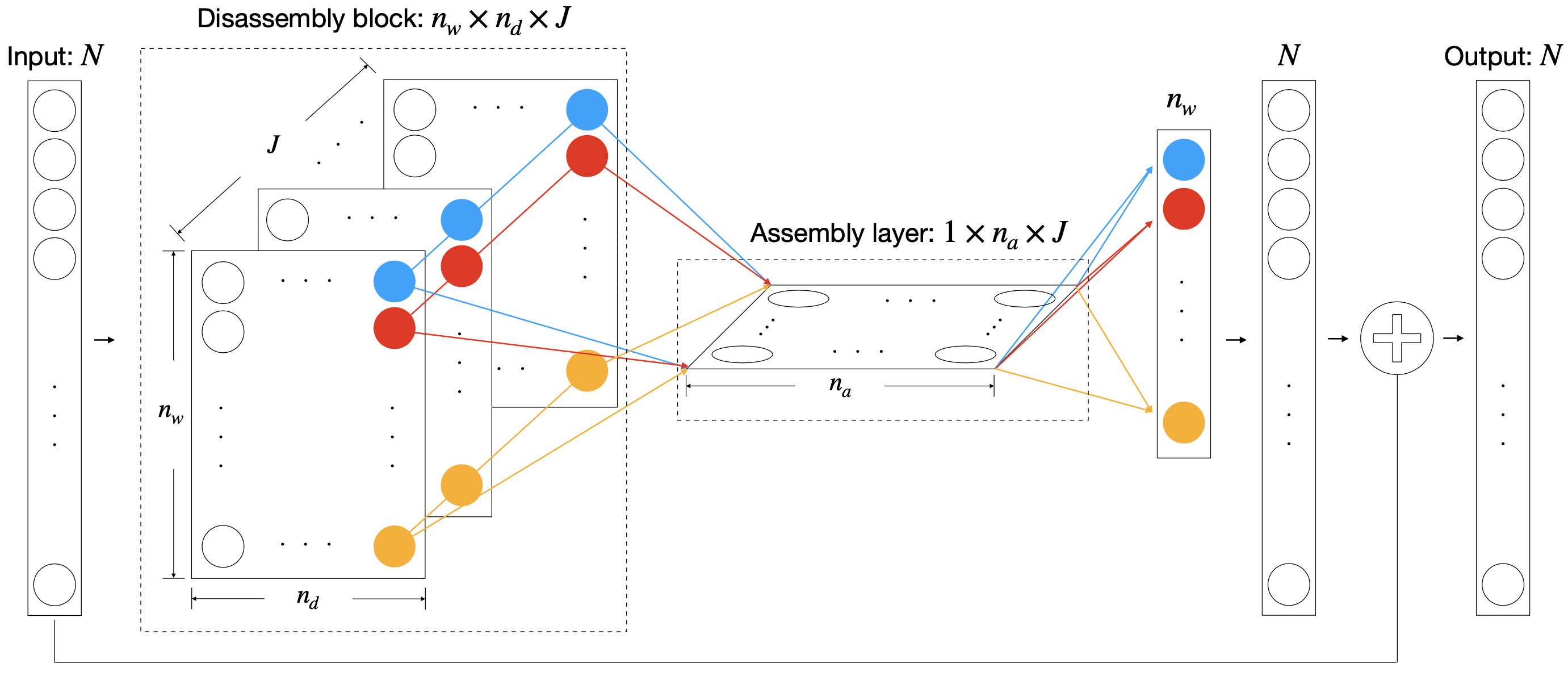 |
| Ensemble Prediction for Robust Learning of Dynamical Systems [arXiv]Because training neural networks relies on stochastic optimization, network predictions follow some high-dimensional probability distribution. Networks trained to sufficient accuracy typically follow distributions with low bias but high variance due to the large number of hyperparameters. This results in unreliable, less accurate predictions. We show via the Central Limit Theorem that ensemble prediction, whereby multiple networks are independently trained and their predictions are averaged at each time step, results in Gaussian-distributed predictions with variance scaling like the reciprocal of the number of models trained. This technique makes predictions significantly more robust and accurate. | 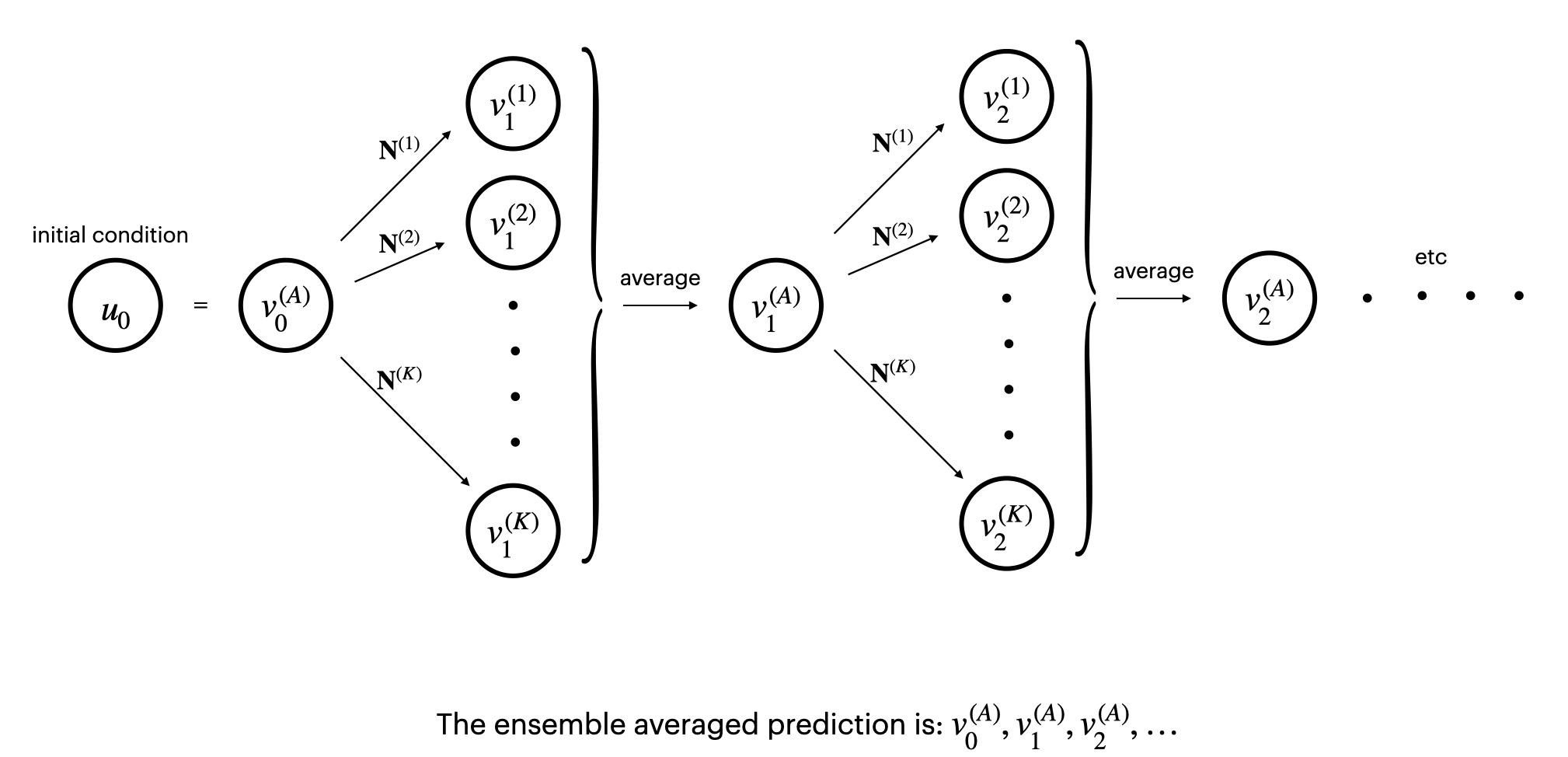 |
| Learning Partially-Observed Chaotic Dynamics [journal] [arXiv] We consider learning the chaotic Lorenz 63 and 96 systems while observing a time-history of only a subset of the state variable solutions. One interesting technical aspect of this work was that instead of many training trajectories starting from randomized initial conditions, we used only a single training trajectory. | 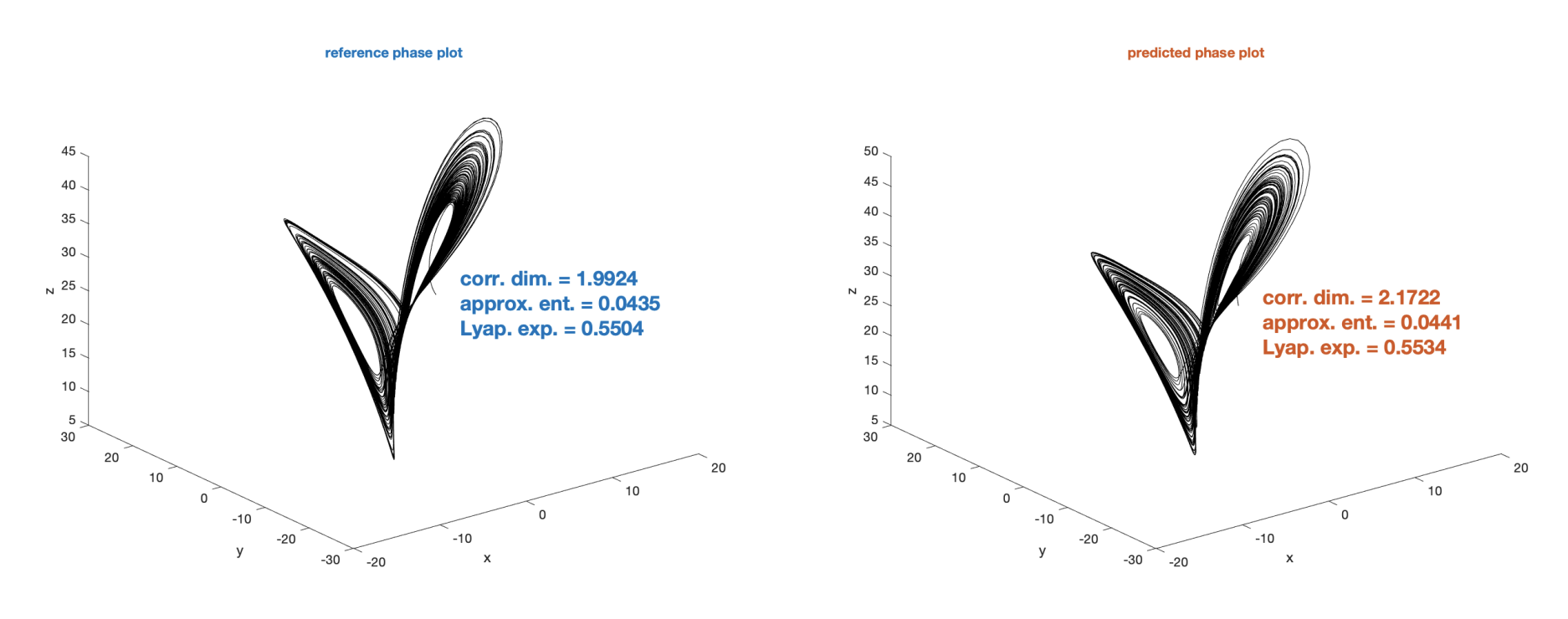 |
| Learning Dynamics for Systems Coarsely-Observed in Time [journal] [arXiv]In real applications, observations may be made on a time scale that is too coarse to properly display smooth system dynamics. This could be due, e.g., to storage or runtime limitations. To address this, we introduce the idea of inner recurrence, which repeatedly convolves the network function with itself to fill the gaps in time with the unique smooth dynamics. | 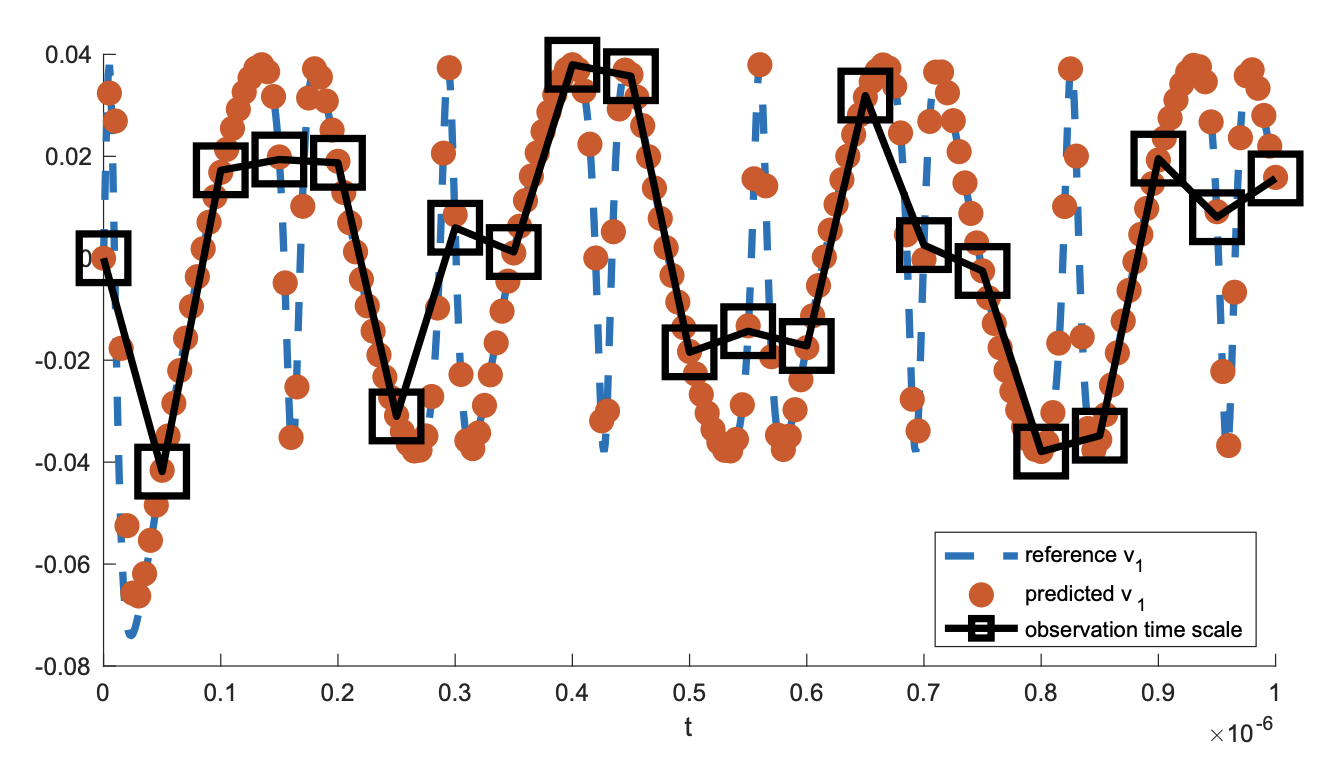 |
| My Ph.D. work was on quantifying uncertainity in inverse problems in imaging. Here's one demonstrative project. |
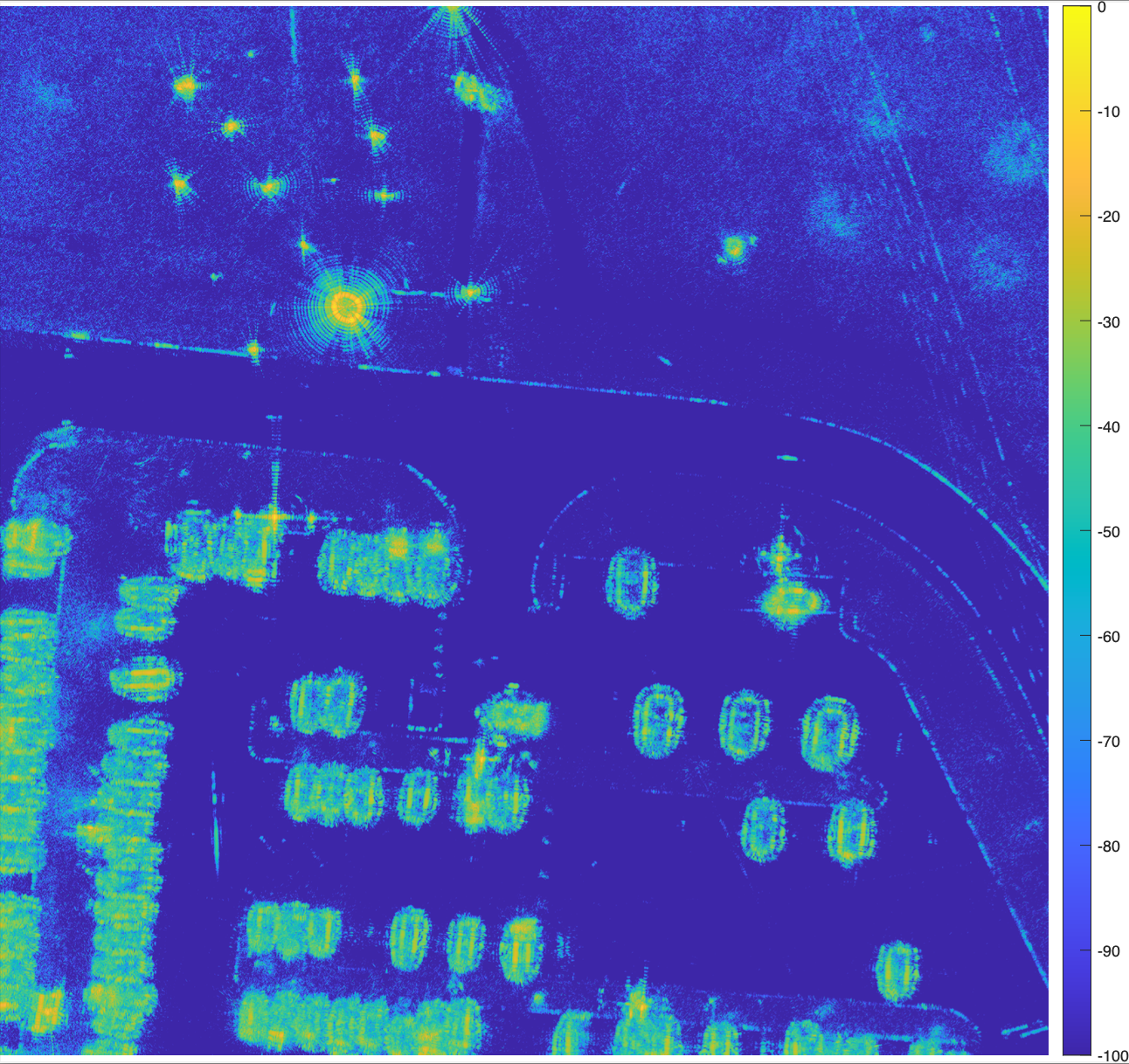
| Sampling-based Radar Image Reconstruction with Uncertainty Quantification [pdf] Typically in radar imaging, only a single maximum a posteriori image estimate is retrieved. The maximum is not a categorically strong representative of the posterior, and provides no uncertainty quantification. Instead, we interrogate the posterior by sampling it using a Gibbs sampler. From the samples, confidence intervals are derived for each pixel value. The image is a parking lot from the GOTCHA SAR data set from Air Force Research Laboratory. |
|
| I have enjoyed teaching and mentoring students of all levels at both Ohio State and Dartmouth. At Ohio State, I have been responsible for both undergraduate and graduate computational science courses. In these courses, my research frequently plays a role in my lecture content in the form of examples, data, and context. Please see my [CV] for more info. |
| I love running and the sport of track and field. My personal bests are: 4:51 for 1 mile, 18:45 for 5000m, 1:27 for the half marathon, and 3:07 for the marathon. My other interests include bonsai, architecture, and animals. At one point, I tried to pull off bleach blonde hair. |
