

Next: About this document ...
Up: No Title
Previous: No Title
- 1
- J.M. Bardeen, B. Carter and S.W. Hawking,
Comm. Math. Phys. 31 161 (1973).
- 2
-
S.W. Hawking, Comm. Math. Phys. 43 199 (1975).
- 3
- J.D. Bekenstein, Phys. Rev. D 7, 2333 (1973).
- 4
- L. Bombelli, R.K. Koul, J. Lee, and R.D. Sorkin,
Phys. Rev. D 34, 373 (1986).
- 5
- Another
argument that might be advanced in support of the
proportionality of entropy and area comes from the holographic
hypothesis[6,7],
ie, the idea that the state of the part of the
universe inside a spatial region can be fully specified
on the boundary of that region. However, currently the
primary support for this hypothesis comes from black hole
thermodynamics itself. Since we are trying to account for the
occurrence of thermodynamic-like laws for classical black
holes it would therefore be circular to invoke this argument.
- 6
- G. `t Hooft, ``Dimensional Reduction in Quantum Gravity",
Utrecht preprint THU-93/26, gr-qc/9310026 .
- 7
- L. Susskind, ``The World as a Hologram",
Stanford preprint SU-ITP-94-33, hep-th/9409089, to appear in
J. Math. Phys., November 1995.
- 8
- W.G. Unruh, Phys. Rev. D 14, 870 (1976).
- 9
- If the entropy density on the horizon takes the form
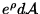 ,
with
,
with 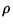 a function of the Ricci scalar,
one finds that
a function of the Ricci scalar,
one finds that 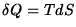 implies
implies
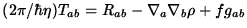 for some function f
[10].
Imposing the local energy conservation equation
for some function f
[10].
Imposing the local energy conservation equation
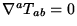 then allows one to solve uniquely for f
up to a constant.
then allows one to solve uniquely for f
up to a constant.
- 10
- T. Jacobson, G. Kang, R.C. Myers,
``Increase of Black Hole Entropy in Higher Curvature Gravity",
McGill preprint
94-95, Maryland preprint UMDGR-95-047, gr-qc/9503020, to be published
in Phys. Rev. D.
- 11
- D.W. Sciama, P. Candelas, and D. Deutsch, Adv. in Phys.,
30, 327 (1981).
FIGURE 1: Spacetime diagram showing the heat flux  across the local Rindler horizon
across the local Rindler horizon  of a 2-surface element
of a 2-surface element
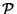 . Each point in the diagram represents a two dimensional
spacelike surface. The hyperbola is a uniformly accelerated worldline,
and
. Each point in the diagram represents a two dimensional
spacelike surface. The hyperbola is a uniformly accelerated worldline,
and 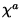 is the approximate boost Killing vector on
is the approximate boost Killing vector on 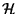 .
.
Ulrich Gerlach
1998-02-13
![]() across the local Rindler horizon
across the local Rindler horizon ![]() of a 2-surface element
of a 2-surface element
![]() . Each point in the diagram represents a two dimensional
spacelike surface. The hyperbola is a uniformly accelerated worldline,
and
. Each point in the diagram represents a two dimensional
spacelike surface. The hyperbola is a uniformly accelerated worldline,
and ![]() is the approximate boost Killing vector on
is the approximate boost Killing vector on ![]() .
.