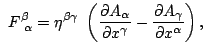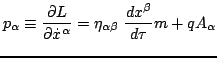


Next: Advantage of the Hamiltonian
Up: Laser-driven particle mechanics
Previous: Motivational Overview
Contents
The action integral for a particle of mass 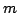 and charge
and charge 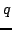 is
is
where
![$ [\eta_{\alpha\beta}]=diag(-1,1,1,1)$](img21.png) and
and 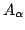 is the
given electromagnetic vector potential. The integral I is an extremum
for those worldlines between
is the
given electromagnetic vector potential. The integral I is an extremum
for those worldlines between
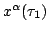 and
and
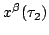 which satisfy the Euler-Lagrange equation
namely,
or
which satisfy the Euler-Lagrange equation
namely,
or
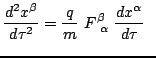
with
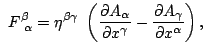
which are the Lorentz equations of motion for the charged particle.
A physically and mathematically more advantageous set of equations is
based on the introduction of the momentum variables
and the superhamiltonian
In terms of these one has the two sets of Hamiltonian equations of motion
One can readily check that this system of first order equations
implies the Euler-Lagrange equations.



Next: Advantage of the Hamiltonian
Up: Laser-driven particle mechanics
Previous: Motivational Overview
Contents
Ulrich Gerlach
2005-11-07
![]() and charge
and charge ![]() is
is
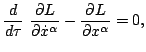
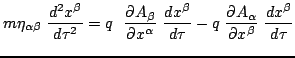
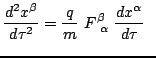 with
with