


Next: The Dynamical Phase
Up: Laser-driven particle mechanics
Previous: Lagrangian and Hamiltonian Formulation
Contents
One of the chief virtues of the Lagrangian equations of motion is that
they remain invariant under an arbitrary point transformation
Hamilton's equations of motion not only share this virtue but they
take it to a higher level: they are invariant under certain more
general transformations
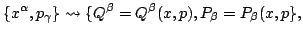 |
(5) |
which is to say,
Here 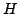 is the transformed superhamiltonian obtained from
is the transformed superhamiltonian obtained from
 with the help of Eq.(5):
Termed canonical, such transformations have the distinguishing property that
they leave invariant the representation of the antisymmetric tensor
with the help of Eq.(5):
Termed canonical, such transformations have the distinguishing property that
they leave invariant the representation of the antisymmetric tensor
A sufficient condition for a transformation,
Eq.(5), to be canonical is that there exist a
scalar function of
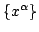 and
and
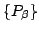 ,
,
Indeed, letting
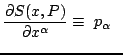 and and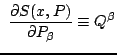 |
(7) |
one finds that
- Problem 1: Prove that
the representation invariance of Eq.(8) implies
the local existence of a scalar
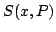 whose gradients yield
Eq.(7).
whose gradients yield
Eq.(7).
Thus the existence of a scalar 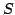 is both a necessary and a sufficient
condition for the invariance expressed by Eq.(8).
It also is a sufficient condition for the invariance of Hamilton's
equations of motion.
is both a necessary and a sufficient
condition for the invariance expressed by Eq.(8).
It also is a sufficient condition for the invariance of Hamilton's
equations of motion.
- Problem 2:
Show that a transformation such as the one given by
Eq.(7) transforms the given euations of motion,
Eqs.(3)-(4), into the same form, and given by
Eq.(6).
Discussion:
Taking advantage of the chain rule, let
be a vector tangent to the phasespace trajectory
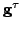 relative to the given (
relative to the given (
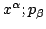 ) and the new (
) and the new (
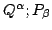 )
coordinates respectively.
)
coordinates respectively.
a) Show that
b) Point out why
c) Show that
implies Hamilton's equations of motion, Eq.(3)-(4).
d) Show that the introduction of the new coordinates
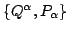 into
into
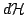 ,
,
yields Eq.(6), Hamilton's equations
relative to the new coordinates
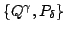 .
.



Next: The Dynamical Phase
Up: Laser-driven particle mechanics
Previous: Lagrangian and Hamiltonian Formulation
Contents
Ulrich Gerlach
2005-11-07
![]() and
and
![]() ,
,
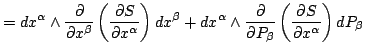
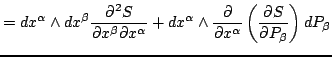
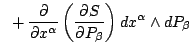
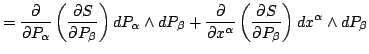
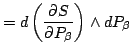
![]() is both a necessary and a sufficient
condition for the invariance expressed by Eq.(8).
It also is a sufficient condition for the invariance of Hamilton's
equations of motion.
is both a necessary and a sufficient
condition for the invariance expressed by Eq.(8).
It also is a sufficient condition for the invariance of Hamilton's
equations of motion.
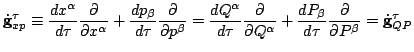
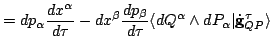
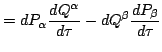
![]() into
into
![]() ,
,