

Next: About this document ...
Up: PAIRED ACCELERATED FRAMES: THE
Previous: PAIRED ACCELERATED FRAMES: THE
Figure 1:
Acceleration-induced partitioning of spacetime into the
four Rindler sectors.
![\begin{figure}
\epsfclipon \setlength{\epsfysize}{3.5in}
\setlength{\epsfxsize...
...
\centerline{\epsffile[0 400 500 680]{four_rindlerssctors_fig1.ps}}
\end{figure}](img31.gif) |
Figure 2:
Two interferometers. The Euclidean interferometer, which
in optics is known as a Mach-Zehnder interferometer, consists of
a half-silvered entrance mirror (thin line at the bottom),
a half-silvered exit mirror (thin line at the top),
and two fully reflecting mirrors (thick lines on the right and the left).
The Lorentzian interferometer consists of the entrance region, Rindler
Sector P,
the exit region, Rindler Sector F, and the two reflective regions,
Rindler Sectors I and II. The reflection is brought about by
by the pseudo-gravitational potential
(see Eq.(14))
in each sector. The thick hyperbolae
separate the region of this potential where the mode is oscillatory
from that region where
it is evanescent. This reflection process is detailed in
Figure 6.
![\begin{figure}
\epsfclipon\epsffile[100 570 500 680]{diagram.ps}\end{figure}](img32.gif) |
Figure:
Pair of monochromatic detectors configured to measure interference
between waves from I and II, Figure (a), or to measure the
amplitude of each waves from I and II separately, Figure (b)
(``delayed choice experiment'').
The detectors are monochromatic because they are surrounded by
interference filters. Each such
filter consists of a Fabry-Perot cavity with uniformly
moving walls. Such a cavity has discrete transmission resonances at
Rindler frequencies given by
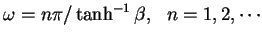 ,
where
,
where 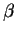 is the relative velocity of the cavity walls.
Their histories delineate the evolution of a cavity's interior
(lightly shaded wedge in the figure).
is the relative velocity of the cavity walls.
Their histories delineate the evolution of a cavity's interior
(lightly shaded wedge in the figure).
![\begin{figure}
\epsfxsize=6in
\epsffile[100 420 612 670]{detectors.ps}\end{figure}](img34.gif) |
Figure 4:
Minkowski-Bessel modes of positive and negative Minkowski frequency,
and the four Rindler coordinate representatives for each.
Note that the ensuing Figures 5
and 6 are mathematically equivalent to the above
figures (Figs. 4a and b). All of them depict
the Minkowski-Bessel modes  .
Figure 6
is obtained by applying to Figure 4 some
well-known identities between Hankel and Bessel functions and between
McDonald and modified Bessel functions. Figures 5
and 6 are equivalent by virtue
of the coordinate transformations in Figure 1
.
Figure 6
is obtained by applying to Figure 4 some
well-known identities between Hankel and Bessel functions and between
McDonald and modified Bessel functions. Figures 5
and 6 are equivalent by virtue
of the coordinate transformations in Figure 1
![\begin{figure}
\setlength{\epsfxsize}{6.0in}
\epsfysize=7in
\centerline{\epsffile[0 100 612 670]{m-b_modes_figs_ab.ps}}
\end{figure}](img35.gif) |
Figure 5:
Amplitude splitting of the Minkowski-Bessel modes of
positive and negative Minkowski frequency. Each mode expresses an interference
process as found in the Mach-Zehnder interferometer familiar from optics.
A wave in P far from the
bifurcation event enters the ``interferometer'' from P.
As indicated by the two heavy arrows, the wave splits
into two partial waves: one propagates from P (tail of the arrow)
across the past event horizon, and enters Rindler Sector I (tip of
the same arrow). There it propagates to the right
under the influence of the familiar boost-invariant pseudo-gravitational
potential. This is shown explicitly in Figure 6.
The wave becomes evanescent (exponentially decaying)
in the shaded hyperbolic region and hence gets reflected
by this potential. Upon propagating to the left the wave
escapes from Rindler Sector I (tail of the next arrow)
through its future event horizon into the future sector F
(tip of that arrow).
There it recombines with the other partial wave which got reflected
in Rindler Sector II.
![\begin{figure}
\epsfclipon\centerline{\epsffile[0 320 612 680]{amplitude_splitting.ps}}
\end{figure}](img36.gif) |
Figure 6:
Reflection of partial waves from their potential barriers
(shaded hyperbolae) in Rindler Sectors I and II. As in
Figure 5, the four arrows connect partial waves
propagating from one Rindler sector to another. In Rindler Sectors
P and F the partial waves are proportional to the Bessel functions
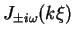 of order
of order 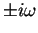 ,
while in I and II
they are proportional to the modified Bessel functions
,
while in I and II
they are proportional to the modified Bessel functions
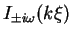 .
The latter oscillate for finite
.
The latter oscillate for finite 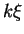 ,
but blow up
exponentially as
,
but blow up
exponentially as
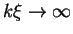 in each hyperbolically
shaded region. The reflection process is brought about by the boundary
condition that the incident wave in I (
in each hyperbolically
shaded region. The reflection process is brought about by the boundary
condition that the incident wave in I (
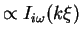 )
must combine with the reflected wave (
)
must combine with the reflected wave (
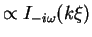 )
so
as to form a total wave whose amplitude approaches zero as
)
so
as to form a total wave whose amplitude approaches zero as
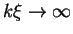 .
This wave is a standing wave (
.
This wave is a standing wave (
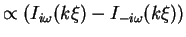 in I and thus expresses a
process of reflection from the boost-invariant pseudo-gravitational
potential.
An analogous reflection process takes place in Rindler Sector II.
in I and thus expresses a
process of reflection from the boost-invariant pseudo-gravitational
potential.
An analogous reflection process takes place in Rindler Sector II.
![\begin{figure}
\epsffile[200 370 712 600]{sidebyside_reflmodea_b.ps}\end{figure}](img37.gif) |
Figure:
WKB-approximate formulas for the Minkowski-Bessel modes. All
formulas assume that
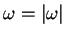 .
The upper (lower)
signs in a picture go only with the upper (lower) signs in the corresponding boxed
formula. This means, for example, that the formula (in all four
Rindler sectors) for a M-B of, say, positive Minkowski frequency and of
negative Rindler frequency, is designated by
.
The upper (lower)
signs in a picture go only with the upper (lower) signs in the corresponding boxed
formula. This means, for example, that the formula (in all four
Rindler sectors) for a M-B of, say, positive Minkowski frequency and of
negative Rindler frequency, is designated by 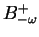 ,
and is
given by the lower signed expressions in the second picture.
The complete propagation process (splitting, reflection, and
interference) of a M-B mode is characterized by the phase
,
and is
given by the lower signed expressions in the second picture.
The complete propagation process (splitting, reflection, and
interference) of a M-B mode is characterized by the phase
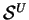 ,
which
is continuous across the U-axis, and the phase
,
which
is continuous across the U-axis, and the phase
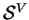 ,
which is
continuous across the V-axis. Both satisfy the Hamilton-Jacobi
equation
,
which is
continuous across the V-axis. Both satisfy the Hamilton-Jacobi
equation
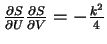 ,
which is implied by Eq.(
,
which is implied by Eq.(![[*]](cross_ref_motif.gif) ). The amplitude
). The amplitude
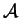 or (
or (
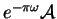 )
of each WKB wave propagating across its respective event horizon satisfies the concomitant conservation law
)
of each WKB wave propagating across its respective event horizon satisfies the concomitant conservation law
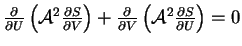 ,
where
,
where
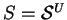 or
or
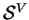 ,
depending on which horizon
is being crossed.
,
depending on which horizon
is being crossed.
![\begin{figure}
\epsfclipon\epsffile[60 400 712 650]{sidebyside_wkb_ab.ps} \epsfverbosetrue
\end{figure}](img46.gif) |
Figure:
Two-dimensional phase space spanned by the Minkowski frequency
parameter 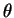 ( Eq.(
( Eq.(![[*]](cross_ref_motif.gif) ) ) and by the
Rindler frequency
) ) and by the
Rindler frequency 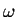 .
The windowed Fourier basis of orthonormal
wavelets ( Eqs.(
.
The windowed Fourier basis of orthonormal
wavelets ( Eqs.(![[*]](cross_ref_motif.gif) )-(
)-(![[*]](cross_ref_motif.gif) ) ) partitions this space into phase space cells
of equal area
) ) partitions this space into phase space cells
of equal area 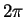 .
The support of each wavelet and its Fourier
transform are concentrated horizontally and vertically within each
dashed rectangle. A heavy dot locates the amplitude maximum of the
corresponding wavelet and its Fourier transform. The shape of the area
elements is controlled by the freely adjustable parameter
.
The support of each wavelet and its Fourier
transform are concentrated horizontally and vertically within each
dashed rectangle. A heavy dot locates the amplitude maximum of the
corresponding wavelet and its Fourier transform. The shape of the area
elements is controlled by the freely adjustable parameter
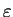 .
Physically it indicates the rate at which each Klein-Gordon
wave packet collapses and explodes.
.
Physically it indicates the rate at which each Klein-Gordon
wave packet collapses and explodes.
![\begin{figure}
\epsfclipon\epsffile[-125 -20 283 268]{cartesian_phasespace.xfig.eps} \epsfverbosetrue
\end{figure}](img47.gif) |
Figure 9:
Two different partitionings of phase space. The elementary
phase space areas have the same magnitude, but their shapes are
different. They are characterized by the explosivity index
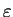 defined in Figure 8. The tall
and skinny elements (
defined in Figure 8. The tall
and skinny elements (
 )
define Klein-Gordon wave
packet histories with well-defined mean Minkowski frequency but
indeterminate Rindler frequency. Such wave packets contract and
reexpand non-relativistically in their respective frames of
reference. By contrast, the short and squatty elements (
)
define Klein-Gordon wave
packet histories with well-defined mean Minkowski frequency but
indeterminate Rindler frequency. Such wave packets contract and
reexpand non-relativistically in their respective frames of
reference. By contrast, the short and squatty elements (
 )
define Klein-Gordon wave packet histories with
well-defined mean Rindler frequency but indeterminate Minkowski
frequency. Such wave packets collapse and reexplode
relativistically in their respective frames of reference.
)
define Klein-Gordon wave packet histories with
well-defined mean Rindler frequency but indeterminate Minkowski
frequency. Such wave packets collapse and reexplode
relativistically in their respective frames of reference.
![\begin{figure}
\epsfclipon\epsffile[-75 -20 392 206]{cells_skinny_and_squatty.xfig.eps} \epsfverbosetrue
\end{figure}](img48.gif) |
Figure:
Double slit interference of two waves
modes entering and emerging from a pair of accelerated frames. In
reality the two figures should be superimposed one on top of the
other. However, for clarity, we show the two waves separately, one
passing through Rindler Sector I (FIGURE B), the other through
Rindler Sector II (FIGURE A). The interference occurs in Rindler
Sector F, where the two waves meet and superpose to form a
resultant wave.
The process of each partial
wave passing through its respective spacetime sector (I and II)
is a reflection process. Each figure depicts the WKB phase fronts
being reflected by the pseudo-gravitational potential. Note that the
direction of propagation of the wave mode is perpendicular (in the
Lorentz sense) to its phase fronts. FIGURE B pictures the reflection
process
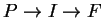 ,
which is expressed by the
wave
,
which is expressed by the
wave
![${\mathcal{A}} \exp [i{\mathcal{S}}^V] +{\mathcal{A}} \exp
[-i{\mathcal{S}}^U]$](img49.gif) ,
the WKB expression for
,
the WKB expression for 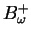 in Figure
7a. The incident wave
in Figure
7a. The incident wave
![${\mathcal{A}} \exp
[-i{\mathcal{S}}^U]$](img50.gif) ,
which propagates from P towards the boundary
(
,
which propagates from P towards the boundary
(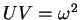 )
of evanescence in Im represented in the figure by
the isograms of
)
of evanescence in Im represented in the figure by
the isograms of
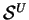 .
Similarly, the reflected wave
.
Similarly, the reflected wave
![${\mathcal{A}} \exp [i{\mathcal{S}}^V]$](img51.gif) ,
which propagates from the
boundary of evanescence in I to the future F, is represented by
the isograms of the phase
,
which propagates from the
boundary of evanescence in I to the future F, is represented by
the isograms of the phase
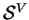 .
Note that the incident
and the reflected phase contours intersect the boundary in a
perpedicular way. In an analogous way, FIGURE A pictures the
reflection process
.
Note that the incident
and the reflected phase contours intersect the boundary in a
perpedicular way. In an analogous way, FIGURE A pictures the
reflection process
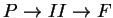 ,
which is
expressed by the wave
,
which is
expressed by the wave
![$e^{-\pi \omega}{\mathcal{A}} \exp
[-i{\mathcal{S}}^U] +e^{-\pi \omega}{\mathcal{A}} \exp
[i{\mathcal{S}}^V]$](img52.gif) ,
the WKB expression for
,
the WKB expression for 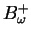 in Figure
7a.
in Figure
7a.
The interference occurs in
Rindler Sector F, where the phase fronts in FIGURE A overlap with
those in FIGURE B.
![\begin{figure}
\epsfclipon\epsfxsize=6in
\epsffile[-50 465 570 732]{sidebyside_refl_phase_inI_II.ps} \epsfverbosetrue
\end{figure}](img53.gif) |


Next: About this document ...
Up: PAIRED ACCELERATED FRAMES: THE
Previous: PAIRED ACCELERATED FRAMES: THE
Ulrich Gerlach
1999-04-15
![\begin{figure}
\epsfclipon \setlength{\epsfysize}{3.5in}
\setlength{\epsfxsize...
...
\centerline{\epsffile[0 400 500 680]{four_rindlerssctors_fig1.ps}}
\end{figure}](img31.gif)
![\begin{figure}
\epsfclipon\epsffile[100 570 500 680]{diagram.ps}\end{figure}](img32.gif)
![\begin{figure}
\epsfxsize=6in
\epsffile[100 420 612 670]{detectors.ps}\end{figure}](img34.gif)
![\begin{figure}
\setlength{\epsfxsize}{6.0in}
\epsfysize=7in
\centerline{\epsffile[0 100 612 670]{m-b_modes_figs_ab.ps}}
\end{figure}](img35.gif)
![\begin{figure}
\epsfclipon\centerline{\epsffile[0 320 612 680]{amplitude_splitting.ps}}
\end{figure}](img36.gif)
![\begin{figure}
\epsffile[200 370 712 600]{sidebyside_reflmodea_b.ps}\end{figure}](img37.gif)
![\begin{figure}
\epsfclipon\epsffile[-75 -20 392 206]{cells_skinny_and_squatty.xfig.eps} \epsfverbosetrue
\end{figure}](img48.gif)
![\begin{figure}
\epsfclipon\epsfxsize=6in
\epsffile[-50 465 570 732]{sidebyside_refl_phase_inI_II.ps} \epsfverbosetrue
\end{figure}](img53.gif)