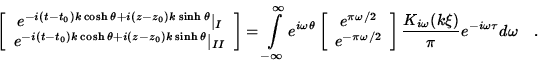

Next: SUMMARY
Up: ACCELERATION-INDUCED CARRIER OF THE
Previous: Geometry of the Space
Our proposal is
to have each spinor field serve as a carrier of the imprints of
gravitation: A gravitational disturbance confined to, say, Rindler
I
or II
would leave its imprint on a spinor field at
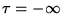 by changing it into another spinor field at
by changing it into another spinor field at
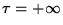 .
.
We know that in the absence of gravitation each of the positive and
negative Minkowski plane wave solutions evolves independently of all
the others. This scenario does not change under Lorentz boosts and
spacetime translations. This is another way of saying that the system
described by these solutions is Poincare invariant. Will the proposed
carriers comply with this invariance, which is stipulated by
fundamental requirement 3.? To find out, consider a typical plane
wave. Its spinor representation (3) is
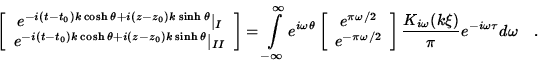 |
10 |
This is a state with 100% correlation between the boost energy and
the polarization (``spin'') degrees of freedom. In recent years such
states have been called ``entangled'' states[12].
Suppose that for each
boost energy we determine the normalized Stokes parameters of this
polarization, i.e. the expectation values of the three modified Pauli
``spin'' matrices
![\begin{displaymath}{\overrightarrow \sigma}:
\{\sigma_1,\sigma_2,\sigma_3\}=\le...
...gin{array}{cc}
1&0 \\
0&-1
\end{array}\right]\right\} \quad .
\end{displaymath}](img25.gif) |
11 |
This is a
three-dimensional vector field over the base manifold R
, and is given by
[13]
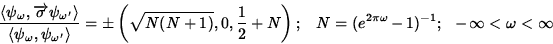 |
12 |
In compliance with requirements 2. and 3., this vector field is (a)
independent of the particle mass and (b) the same for all
positive (negative) Minkowski plane wave modes, a fact which expresses
its Poincare invariance. The presence of gravitation would leave
its imprints by producing characteristic alterations in this vector
field.


Next: SUMMARY
Up: ACCELERATION-INDUCED CARRIER OF THE
Previous: Geometry of the Space
Ulrich Gerlach
1998-02-20
![]() by changing it into another spinor field at
by changing it into another spinor field at
![]() .
.