

Next: Quantum Mechanical Carrier of
Up: ACCELERATION-INDUCED CARRIER OF THE
Previous: Relativistic Quantum Mechanics
The representation (3) puts us at an important mathematical juncture:
We shall forego the usual picture of viewing this solution as an
element of Hilbert space (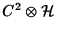 ) with the Klein-Gordon
inner product,
) with the Klein-Gordon
inner product,
Instead, we shall adopt a qualitatively new and superior viewpoint.
Each Klein-Gordon solution is a spinor field over the Rindler
frequency domain. This is
based on the vector bundle 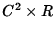 . Here C2
is the complex
vector space of two-spinors, which is the fiber over the
one-dimensional base manifold
. Here C2
is the complex
vector space of two-spinors, which is the fiber over the
one-dimensional base manifold 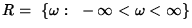 , the real line of Rindler frequencies in the mode integral,
Eq.(3).
, the real line of Rindler frequencies in the mode integral,
Eq.(3).
We know that one can add vectors in the same vector (fiber)
space. However, one may not, in general, add vectors belonging to
different vector spaces at different 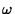 's. The exception is when
vectors in different vector spaces are parallel. In that case
one may add these vectors. The superposition of modes, Eq.(3),
demands that one do precisely that in order to obtain the two
respective total amplitudes of Eq.(3). In
brief, we are about to show that that the linear superposition principle
determines a unique law of parallel transport.
's. The exception is when
vectors in different vector spaces are parallel. In that case
one may add these vectors. The superposition of modes, Eq.(3),
demands that one do precisely that in order to obtain the two
respective total amplitudes of Eq.(3). In
brief, we are about to show that that the linear superposition principle
determines a unique law of parallel transport.
The mode representation of Eq.(3) determines two parallel basis spinor
fields over R
,
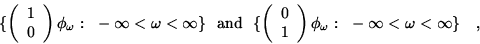 |
6 |
one corresponding to ``spin up'' (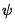 has zero support in Rindler II
),
the other to ``spin down'' (
has zero support in Rindler II
),
the other to ``spin down'' (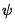 has zero support in Rindler I
).
This parallelism is dictated by the superposition principle, Eq.(3):
The total amplitude at a point
has zero support in Rindler I
).
This parallelism is dictated by the superposition principle, Eq.(3):
The total amplitude at a point 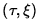 in Rindler I
(resp. II
)
is obtained by adding all the contributions from Rindler I
(resp. II
)
only.
in Rindler I
(resp. II
)
is obtained by adding all the contributions from Rindler I
(resp. II
)
only.
One can see from Eq.(6) that, relative to this
basis, the fiber metric over each 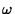 is given by
is given by
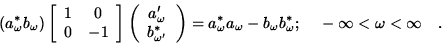 |
7 |
It is evident that the law of parallel transport defined by
Eq.(7) is compatible with this
(Klein-Gordon induced) fiber metric. This is because the two parallel
vector fields, which are represented by
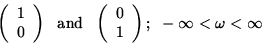 |
8 |
relative to the basis (7), are orthonormal with respect to the
the fiber
metric Eq.(8) at each point 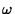 of the base space R
.
It is not difficult to verify that these two spinor fields
are (Klein-Gordon) orthonormal in each fiber over R
. The spinor
field
of the base space R
.
It is not difficult to verify that these two spinor fields
are (Klein-Gordon) orthonormal in each fiber over R
. The spinor
field
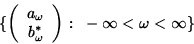 |
9 |
is a section of the fiber bundle 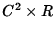 and it represents a
linear combination of the two parallel vector fields. It is clear that
there is a one-to-one correspondence between
and it represents a
linear combination of the two parallel vector fields. It is clear that
there is a one-to-one correspondence between 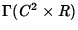 ,
the
,
the 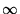 -dimensional space of sections of this spinor bundle, and
the space of solutions to the Klein-Gordon equation.
-dimensional space of sections of this spinor bundle, and
the space of solutions to the Klein-Gordon equation.


Next: Quantum Mechanical Carrier of
Up: ACCELERATION-INDUCED CARRIER OF THE
Previous: Relativistic Quantum Mechanics
Ulrich Gerlach
1998-02-20
![]() ) with the Klein-Gordon
inner product,
) with the Klein-Gordon
inner product,
![]() 's. The exception is when
vectors in different vector spaces are parallel. In that case
one may add these vectors. The superposition of modes, Eq.(3),
demands that one do precisely that in order to obtain the two
respective total amplitudes of Eq.(3). In
brief, we are about to show that that the linear superposition principle
determines a unique law of parallel transport.
's. The exception is when
vectors in different vector spaces are parallel. In that case
one may add these vectors. The superposition of modes, Eq.(3),
demands that one do precisely that in order to obtain the two
respective total amplitudes of Eq.(3). In
brief, we are about to show that that the linear superposition principle
determines a unique law of parallel transport.
![]() is given by
is given by