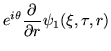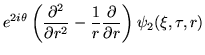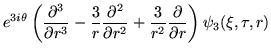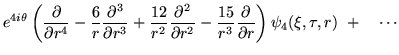

Next: RADIATION: PHYSICAL RELATION TO
Up: Full Scalar Radiation Field
Previous: Source as a Sum
The field is a superposition of multipole field amplitudes. The first
few terms of this superposition are
whose explicit form is
where
It is evident that each multipole term has its own distinguishing angular (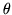 ) and radial (
) and radial (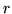 ) dependence.
) dependence.


Next: RADIATION: PHYSICAL RELATION TO
Up: Full Scalar Radiation Field
Previous: Source as a Sum
Ulrich Gerlach
2001-10-09