Construction

The formation of this concept is achieved by using one of the clocks, say $R$, as a reference clock which measures and collects two kinds of data about all the other clocks, say $A,B,C,\cdots$ : Doppler shifts and instantaneous distance of $A,B,C,\cdots$ from $R$.

Doppler shift measurements are frequency measurements. The emission frequencies of all clocks $A,B,C,\cdots$ are the same, say $\omega_0$. Consequently, the frequencies $\omega_A,\omega_B,\omega_C,\cdots$ received and measured by $R$ yield the corresponding Doppler shift factors

$$k_A=\frac{\omega_A}{\omega_0}\equiv \exp{(-\tau_A)}, ~k_B=\f... ...~ k_C=\frac{\omega_C}{\omega_0}\equiv \exp{(-\tau_C)},~ \cdots$$

for the respective clocks. From these Doppler shift factors one obtains the relative velocities

$$v_A=\frac{\displaystyle\frac{1}{k_A}-k_A}{\displaystyle\frac... ...k_B}{\displaystyle\frac{1}{k_B}+k_B}\equiv \tanh \tau_B,~ etc.$$

between $R$ and the respective clocks.

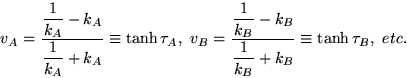
The second kind of measurement is the instantaneous separation. Suppose at some instant of time, say $t_R$, $R$ measures the distances $d_A,d_B,d_C, \cdots$ between $R$ and the clocks $A,B,C,\cdots$. One way of doing this is to have $R$ operate his transmitter and receiver as a radar device.

We now say that $A$ is equivalent to $B$, or more briefly $A\sim B$, if

$$\frac{d_A}{v_A}= \frac{d_B}{v_B}\equiv \xi (t_R)~.$$ (1)

It follows that

1.

$A\sim B$ implies $B\sim A$ and

2.

$A\sim B$ and $B\sim C$ imply $A\sim C$.

By retaining the distinguishing property, the equality of the ratios, Eq.(1), while omitting reference to the particular measurements $d_A,d_B,d_C, \cdots$ and $k_A,k_B,k_C,\cdots$ one forms an equivalence class, the concept ``expanding inertial frame''. It should be noted that the reference clock $R$ is always a member of this equivalence class. This is because, with $d_R=0$ and $v_R=0$, the equivalence condition

$$\frac{d_R}{v_R}= \frac{d_B}{v_B}$$

is satisfied trivially.

The properties of this equivalence class do not depend on the time at which $R$ makes the distance measurements and hence not on the value of the ratio $\xi(t_R)$. Indeed, if instead of $t_R$ that time had been , say $t'_R$, then the corresponding distance measurements would be $d'_A,d'_B,d'_C, \cdots$, then one would still have a set of equal ratios

$$\frac{d'_A}{v_A}= \frac{d'_B}{v_B}\equiv \xi (t'_R)~,$$

which would yield the same equivalence class of free float clocks.

The purpose of an inertial reference frame is for a physicist/observer to use its recording clocks to measure time and space displacements. These measurements consist of establishing quantitative relationships (typically via counting) to a standard which serves as a unit. For a time measurement the unit is the standard interval between any two successive ticks of a clock. For a space measurement the unit is the (logarithm of the) standard Doppler shift factor between any pair of nearest neighbor clocks. Thus the array of clocks forms a lattice which is periodic but is expanding uniformly: the recession velocity between any neighboring pair of clocks is one and the same. This periodicity is an obvious but tacit stipulation in what is meant by ``expanding inertial frame''. Because of this property any one of the recording clocks $A,B,C,\cdots$ can play the role of the reference clock $R$, which is to say that the equivalence relation, Eq.(1), is independent of the choice of $R$.

The two kinds of measurements which gave rise to the equivalence relation between recording clocks also serve to synchronize their operations. Every clock synchronizes itself to its nearest neighbor by setting its own clock reading to the ratio of (i) the nearest neighbor distance and (ii) the Doppler shift determined velocity. Thus the common ratio, Eq.(1), is the synchronous time common to all recording clocks. This common time has an obvious interpretation: The straight-line extensions into the past of all clock histories intersect simultaneously in a common point. This is a singular event, which corresponds to $\xi=0$. The common synchronous time of these clocks is the elapsed proper time since then. However, it is obvious that this singular event is irrelevant for the definition of the expanding inertial frame. What is relevant instead is the ability of the recording clocks to measure Doppler shifts and distances, which presupposes that $\xi \neq 0$. In fact, these clocks might not even have existed until they performed their measurements.

Having constructed the spacetime measuring apparatus, we indicate in general terms how to make spacetime measurements of particles and fields.