Transmission Fidelity

The transfer of information from a transmitter to a receiver, or a system of receivers, depends on being able to establish a one to one correspondence between (i) the phase and amplitude of the e.m. source and (ii) the e.m. signals detected by the observer who mans the receiver(s) in his frame of reference. For a localized source with a straight worldline that frame is static and inertial. For a source with a hyperbolic worldline as in Figure 1, it is expanding and inertial. The e.m. signals are detected by having the recording clocks sample and measure the e.m. field at any fixed synchronous time $\xi>0$. Except for a $\xi$-dependent amplitude and domain shift, these measured field values (along the spatial domain $-\infty<\tau<\infty$) are precisely the values of the current source (along the temporal domain $-\infty<\tau'<\infty$) of the accelerated transmitter[#!notation!#]. Geometrically one says that the transmitter signal-function, whose domain is a timelike hyperbola in Rindler sector $I$, coincides in essence with the receiver signal function whose domain is a spacelike hyperbola in Rindler sector $F$. Thus, if the signal-function is monochromatic at the transmitter end, then so is the signal function on the spatial domain at the receiver end. There is no chirp (changing wave length) in the spatial wave pattern in the expanding inertial frame.

One arrives at that conclusion by verifying it for wave packets, i.e. for narrow but finite pulses of nearly monochromatic radiation, which make up the e.m. signal. Thus consider a uniformly and linearly accelerated transmitter. The history of its center of mass is represented by a timelike hyperbola in, say, Rindler sector $I$ in Figure 1.

Let us have this single transmitter emit two successive pulses which have the same mean frequency and require that they be received at the same synchronous time $\xi$ by two adjacent recording clocks in $F$. One has therefore two well-defined emission-reception processes,

$$(\tau'_A,\xi'):A(\tau'_A,\xi') \begin{array}{c} \textrm{wo... ...arrow\\ \textrm{ } \end{array} (\xi,\tau_A):A(\xi,\tau_A)$$ (2)

and

$$(\tau'_B,\xi'):B(\tau'_B,\xi') \begin{array}{c} \textrm{wo... ...rrow\\ \textrm{ } \end{array} (\xi,\tau_B):B(\xi,\tau_B)~.$$ (3)

Each starts with a pulse emitted by the accelerated transmitter in Rindler sector $I$ and ends with the pulse's reception by an inertial recording clock in Rindler sector $F$. Both processes end with the simultaneous reception of these pulses in the expanding inertial reference frame. Among its recording clocks there are precisely two, labelled by $\tau_A$ and $\tau_B$, which receive pulses $A$ and $B$.

The first process starts with pulse $A$ at event $(\tau'_A,\xi')$ on the timelike hyperbolic world line $\xi'=const'.$ in Rindler sector $I$. That pulse is launched from the instantaneous Lorentz frame $A(\tau'_A,\xi')$ centered around this event. Having traced out its world history across the future event horizon of $I$, this pulse ends the first process at event $(\xi,\tau_A)$ on the spacelike hyperbola of synchronous time $\xi=const.$ There, in the local Lorentz frame $A(\xi,\tau_A)$ of the inertial recording clock with label $\tau=\tau_A$, the (mean) wavelength of the pulse is measured and recorded.

The second process starts with pulse $B$ emitted at event $(\tau'_B,\xi')$ on the same timelike hyperbola $\xi'=const'.$ but at different Rindler time $\tau'=\tau'_B$. This pulse also traces out a world history across the future event horizon. But the end of this pulse is at $(\xi,\tau_B)$ on the same spacelike hyperbola $\xi=const.$ There the (mean) wavelength of the pulse gets measured relative the local Lorentz frame $B(\xi,\tau_B)$ of the inertial recording clock with different label $\tau=\tau_B$. Even though pulses $A$ and $B$ are emitted sequentially by one and the same transmitter, they are received simultaneously by two different recording clocks. This is made possible by the fact that the clock labelled by $\tau_B$ is moving towards the approaching pulse $B$. The blueshift resulting from this motion precisely compensates the redshift which pulse $B$ has relative to $A$ if the recording clock did not have this motion. Thus recording clocks $\tau_A$ and $\tau_B$ receive pulses $A$ and $B$ having precisely the same respective frequencies. This agreement is guaranteed by the principle of relativity. Indeed, Eq.(2) is a Lorentz transform of (3). Each consists of two events, two sets of frame vectors, and a straight pulse history. The Lorentz transformation maps these five entities associated with pulse $A$ into those associated with pulse $B$:

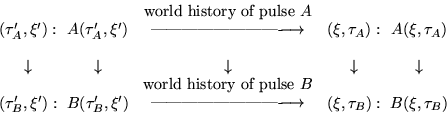$$\begin{array}{ccccc} (\tau'_A,\xi'):&A(\tau'_A,\xi')& \begi... ...extrm{ } \end{array} & (\xi,\tau_B):&B(\xi,\tau_B) \end{array}$$ (4)

Thus the relative velocity, and hence the Doppler shift between frames $A(\xi',\tau'_A)$ and $A(\xi,\tau_A)$, is the same as that between $B(\tau'_B,\xi')$ and $B(\xi,\tau_B)$. This means that the wavelengths of the two received pulses at clock $A(\tau_A)$ and clock $B(\tau_B)$ are the same. There is no Doppler chirp in the composite spatial profile of the received e.m. field at fixed synchronous time $\xi$. If the emitted signal is monochromatic relative to the accelerated transmitter in $I$, then so is the spatial amplitude profile of the received signal relative to the expanding inertial frame in $F$. The transmission of a sequence of pulses is achieved with 100% fidelity.

This conclusion applies to all wavepackets. It also applies to any signal. This is because it is a linear superposition of such packets. A precise mathematical formulation of the emission of signals and their fidelity in transit from an accelerated source to an expanding inertial frame is developed in Section VIA.

Some authors thought that there is some sort of a disconnect between mathematics and physics, in particular between computations and what the computations refer to. For example, they claimed that ``$\cdots$ the coordinates that we use [for computation] are arbitrary and have no physical meaning''[#!Wigner1980!#] or ``It is the very gist of relativity that anybody may use any frame [in his computations].''[#!Schroedinger1956!#] Without delving into the epistemological fallacies underlying these claims, one should be aware of their unfortunate consequences. They tend to discourage attempts to understand natural processes whose very existence and identity one learns through measurements and computations based on nonarbitrary coordinate frames. The identification of radiation from violently accelerated bodies is a case in point. For these, two complementary frames are necessary: an accelerated frame to accommodate the source (Rindler sector $I$ and/or $II$) and the corresponding expanding inertial frame (Rindler sector $F$) to observe the information carried by the radiation coming from this source. These frames are physically and geometrically distinct from static inertial frames. They also provide the logical connecting link between the concepts and the perceptual manifestations (measurements) of these radiation processes. Without these frames the concepts would not be concepts but mere floating abstractions.