


Next: Accelerated Clock
Up: The Radar Method
Previous: The Radar Method
Contents
If B is controlled
by the ticking of an inertially expanding clock, then these events are
These two events are marked by a square and a diamond in Figure
9. The constant 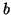 is the proper time
corresponding to
is the proper time
corresponding to 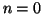 .
.
It follows from Eqs.(12) that the scattering
event measured by B is
These three events, 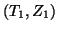 ,
, 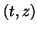 and
and 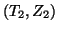 , are marked in
Figure 9 by a square, a circle, and a
diamond.
, are marked in
Figure 9 by a square, a circle, and a
diamond.
Ulrich Gerlach
2003-02-25