


Next: IDENTICALLY CONSTRUCTED CLOCKS AS
Up: MEASURING EVENTS VIA RADAR
Previous: The Common (Non-Radar) Method
Contents
Its Equivalence With The Radar Method
Now compare Eq.(16) with
Eqs.(18) and (13) or
Eq.(17) with Eqs.(18) and (14). Observe that for both
cases
![[*]](footnote.png)
One sees that the radar method is equivalent to the common method
provided one identifies the radar pulse data 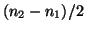 with the
with the
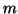 th distant clock, and
th distant clock, and 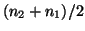 with its
with its 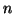 th ticking event.
This equivalence is new. It extends the fundamental and familiar
result based on a lattice array of free-float clocks to (i) the case
of an array of inertially expanding clocks and to (ii) the case of a
array of accelerated clocks. Put differently, it gives physical
validity to the concepts ``inertially expanding frame'' and
``accelerated frame''.
th ticking event.
This equivalence is new. It extends the fundamental and familiar
result based on a lattice array of free-float clocks to (i) the case
of an array of inertially expanding clocks and to (ii) the case of a
array of accelerated clocks. Put differently, it gives physical
validity to the concepts ``inertially expanding frame'' and
``accelerated frame''.
Figure 9:
Lattice of spacetime
graduation events (heavy dots) determined and calibrated by a
single geometrical clock AB which is expanding inertially. The
spacetime history of the e.m. pulse bouncing inside this clock is the
heavy zig zag line left of the middle. The clock is bounded by two
straight lines A and B, the histories of the receding reflectors which
keep the e.m. pulse trapped inside the clock. The other straight
lines indicate the receding reflector histories of identically
constructed clocks, if they were to form an array of adjacent
geometrical clocks. The hyperbolas (dashed lines) are the times
simultaneous with the tickings of the standard clock AB. The 45 lines emanating to the left from A and to the right from B are the
histories of the two trains of pulses escaping from A and B. The fact
that AB is a standard clock implies that all graduation events of the
calibrated lattice lie on these histories. Based on the
method of pulsed radar, each graduation event (e.g. the encircled dot)
is labelled by two unique integers, namely two numbered ticks (the
dots in the square and in the diamond) of the clock.They are AB's
``radar coordinates'' of that graduation event.
lines emanating to the left from A and to the right from B are the
histories of the two trains of pulses escaping from A and B. The fact
that AB is a standard clock implies that all graduation events of the
calibrated lattice lie on these histories. Based on the
method of pulsed radar, each graduation event (e.g. the encircled dot)
is labelled by two unique integers, namely two numbered ticks (the
dots in the square and in the diamond) of the clock.They are AB's
``radar coordinates'' of that graduation event.
![\includegraphics[scale=.6]{array_of_expanding_clocks}](img135.png) |
Figure 10:
Lattice of spacetime
graduation events (heavy dots) as determined and calibrated by a
single geometrical clock CD which is accelerating. The spacetime
history of the e.m. pulse bouncing inside this clock is the heavy zig
zag line between the two hyperbolas C and D. The clock is bounded by
these two hyperbolas, the histories of the two accelerating reflectors
which keep the e.m. pulse trapped inside the clock. The other
hyperbolas indicate the accelerated reflector histories of identically
constructed clocks, if they were to form an array of adjacent
geometrical clocks. The straight lines (lightly dotted) are the times
simultaneous with the tickings of the standard clock CD. The 45 lines emanating to the left from C and to the right from D are the
histories of the two trains of pulses escaping from C and D, with
those escaping from C ultimately crossing the event horizon of clock
CD. The fact that CD is a standard clock implies that all graduation
events of the calibrated lattice lie on these histories. Based on the
method of pulsed radar, each graduation event (e.g. the encircled dot)
is labelled by two unique integers, namely two numbered ticks (the
dots in the square and in the diamond) of the clock. They are CD's
``radar coordinates'' of that graduation event.
lines emanating to the left from C and to the right from D are the
histories of the two trains of pulses escaping from C and D, with
those escaping from C ultimately crossing the event horizon of clock
CD. The fact that CD is a standard clock implies that all graduation
events of the calibrated lattice lie on these histories. Based on the
method of pulsed radar, each graduation event (e.g. the encircled dot)
is labelled by two unique integers, namely two numbered ticks (the
dots in the square and in the diamond) of the clock. They are CD's
``radar coordinates'' of that graduation event.
![\includegraphics[scale=.765]{array_of_accelerated_clocks}](img136.png) |



Next: IDENTICALLY CONSTRUCTED CLOCKS AS
Up: MEASURING EVENTS VIA RADAR
Previous: The Common (Non-Radar) Method
Contents
Ulrich Gerlach
2003-02-25
![[*]](footnote.png)
![[*]](footnote.png)
![\includegraphics[scale=.6]{array_of_expanding_clocks}](img135.png)
![\includegraphics[scale=.765]{array_of_accelerated_clocks}](img136.png)