


Next: PRINCIPLES OF MEASUREMENT
Up: GEOMETRICAL CLOCKS
Previous: Fourier Compatibility
Contents
Time and space acquire their meaning from measurements,
i.e. identifications of a relationship by means of a unit that
serves as a standard of measurement. The measurement process we shall
focus on is based on the emission, reflection, and reception of radar
pulses generated by a standard geometrical clock.
Such a clock consists of a pair of Fourier compatible radar units,
say, A and B. Their reflective surfaces form the two ends of a
one-dimensional cavity with its evenly spaced spectrum of allowed
standing wave modes in between. The operation of the geometrical clock
hinges on having an electromagnetic pulse travel back and forth
between the reflective ends of the cavity. The back and forth travel
rate is determined by the separation between the cavity ends. This
rate need not, of course, be constant in relation to the atomic clocks
carried at either end. A geometrical clock with mutually receding ends
would exemplify such a circumstance.
The definition of a geometrical clock is therefore this: it is a
one-dimensional cavity
- whose bounding ends are Fourier compatible and
- which accommodates an electromagnetic pulse bouncing back and forth
between the left and right end of the cavity.
This bouncing action forms the tick-tock events of the clock. If the cavity
is expanding inertially, these events are located at
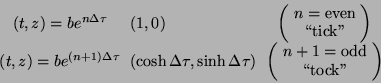 |
(2) |
along the two straight world lines of radar units A and B in spacetime
sector  . Here
. Here
is the Doppler frequency shift factor and 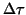 is the fixed
comoving separation between A and B. The constant
is the fixed
comoving separation between A and B. The constant 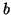 is the Minkowski time
when the geometrical clock strikes zero.
is the Minkowski time
when the geometrical clock strikes zero.
For a clock with ends subjected to accelerations 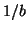 and
and
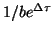 , the ticking events are located at
, the ticking events are located at
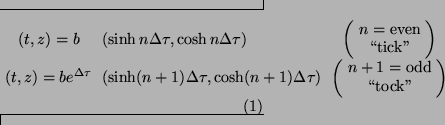
along the two hyperbolic world lines of A and B in boost-invariant sector  .
Here
.
Here
is the pseudo-gravitational frequency shift factor between them, and
 is the boost time between a ``tick'' and a ``tock''.
is the boost time between a ``tick'' and a ``tock''.
The spacetime history of such clocks and their bouncing pulses are
exhibited in Figures 2 and 3.
Figure 2:
Spacetime history of
an inertially expanding clock and the null trajectories of trains of
emitted and received pulses (light lines) whose emission and
reception is controlled by the internal pulse (heavy line) bouncing
back and forth between A and B.
![\includegraphics[scale=.5]{inertial_clock_plus_nullrays}](img47.png) |
Figure 3:
Spacetime history
of an accelerated clock and the null trajectories of trains of
emitted and received pulses (light lines) whose emission and reception is controlled by the
internal pulse (heavy line) bouncing back and forth between A and B.
![\includegraphics[scale=.5]{accelerated_clock_plus_nullrays}](img48.png) |
To serve its purpose, a geometrical clock AB emits and receives pulses
of radiation. When the internal pulse strikes radar unit A its
transmitter and its receiver are turned on only for the duration of
the pulse. This causes A to emit a pulse and to register the reception
of a pulse from the outside, if there is one coming. When the internal
pulse has bounced back to B, an analogous emission and reception
process takes place at radar unit B. It follows that that the
tick-tock action of the internally bouncing clock pulse determines a
set of external pulses moving to the right and to the left. The
history of these pulses together with the clock that controls them is
depicted by Figures 2 and
3 for an inertially expanding and
accelerating clock respectively.



Next: PRINCIPLES OF MEASUREMENT
Up: GEOMETRICAL CLOCKS
Previous: Fourier Compatibility
Contents
Ulrich Gerlach
2003-02-25
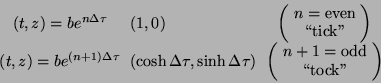
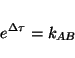
![]() and
and
![]() , the ticking events are located at
, the ticking events are located at
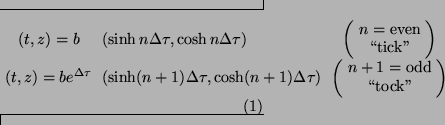
![]() .
Here
.
Here
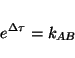
![\includegraphics[scale=.5]{inertial_clock_plus_nullrays}](img47.png)
![\includegraphics[scale=.5]{accelerated_clock_plus_nullrays}](img48.png)