Hardy-Littlewood $k$-tuple Conjecture
By: Mahesh Dhulipala
Over the Summer and Fall of 2016, I worked with Dr. Hiary on modeling the error
term of the Hardy-Littlewood $k$-tuple Conjecture. This conjecture estimates the
number of prime constellations in a given range from $2$ to $N$ (where $N$ is a
large positive integer). A prime constellation is defined as the set of prime
numbers of the form
$$(p,\, p+2m_1,\, p+2m_2,\,\, \ldots\,,\, p+2m_k)$$
where
$m_1,m_2,\ldots,m_k$ are positive integers. The formula for the
conjecture itself is given in the summary report. After some preliminary
research, we guessed that the error term is bounded by something of the
form $AN^{\alpha}$, where $A$ is a constant. To find the value of $\alpha$, we
isolated it using the approximation:
$$\alpha\approx \alpha_{\textrm{approx}} = \frac{\log|\textrm{Empirical} -\textrm{Conjecture}|}{\log N}.$$
The table 1 below shows the behavior of $\alpha_{\textrm{approx}}$ in the
case of the $2$-tuple conjecture for
various values of $N$ and $m_1$. Henceforth, we denote $m_1$ by $r$.
As the graphs show, $\alpha$ seems to be bounded by $1/2$. (Note that the last
three graphs are plotted on logarithmic scale.) Setting $\alpha=1/2$,
we calculated the value of $A$ for various values of $N$. These results are presented in table 2 below, and they suggests that $A$ is inversely
proportional to $N$, decaying with $N$ like an inverse power of $\log N$ perhaps. So $A$ is not a constant independent of $N$ after all, but
bears some relation to it. This suggests that the initial guess for the upper
bound, $AN^{\alpha}$, can be refined. Since we
aimed to estimate the maximum error in the conjecture, we calculated the values
of $A$ for various $N\ge 2^{20}$. The table of the resulting values of $A$ is
given
below in table 3.
Table 1: Graphs of $\alpha_{\textrm{approx}}$
| $N$ | $r$ | Graph |
| $2^{24}$ | 1 to 100 | 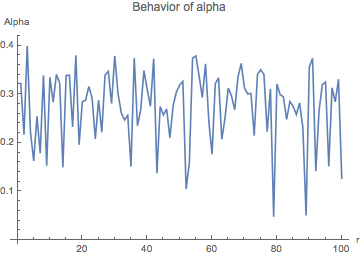 |
| $2^{28}$ | 1 to 100 | 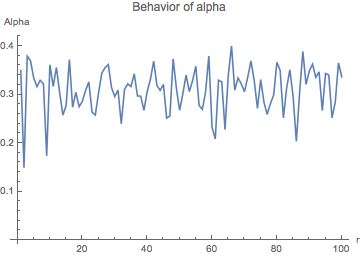 |
| $2^{24}$ |
2 to $2^{100}$ | 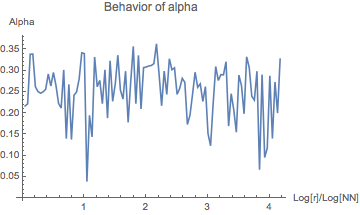 |
| $2^{28}$ | 2 to $2^{100}$ | 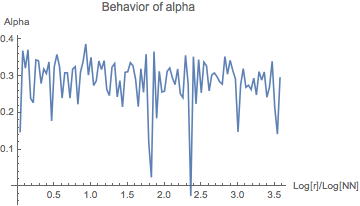 |
| $2^{30}$ | $2^{20}$ to $2^{30}$ | 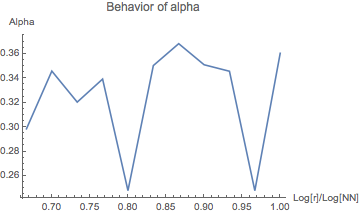 |
Table 2: Behavior of $A$ ($r=2$)
| $N$ | $A$ |
| $2^{20}$ | 3.84914$\times 10^{-5}$ |
| $2^{21}$ | 1.98577$\times 10^{-5}$ |
| $2^{22}$ | 5.50649$\times 10^{-6}$ |
| $2^{23}$ | 8.85031$\times 10^{-6}$ |
| $2^{24}$ | 1.0991$\times 10^{-6}$ |
Table 3: Values of $A$ ($N=2^{20}$)
| $r$ | $A$ |
| 1 | 2.21274$\times 10^{-5}$ |
| 2 | 3.84914$\times 10^{-5}$ |
| 3 | 4.60216$\times 10^{-5}$ |
| 4 | 3.86429$\times 10^{-6}$ |
| 5 | 2.69231$\times 10^{-5}$ |
| 6 | 4.84824$\times 10^{-5}$ |
| 7 | 1.37947$\times 10^{-5}$ |
| 8 | 1.56882$\times 10^{-5}$ |
| 9 | 1.78449$\times 10^{-5}$ |
| 10 | 2.3626$\times 10^{-6}$ |
| 11 | 4.06328$\times 10^{-6}$ |
| 12 | 7.22066$\times 10^{-5}$ |
| 13 | 2.52207$\times 10^{-5}$ |
| 14 | 4.79284$\times 10^{-5}$ |
| 15 | 7.09623$\times 10^{-6}$ |
| 16 | 1.65303$\times 10^{-5}$ |
| 17 | 1.78241$\times 10^{-5}$ |
| 18 | 1.85252$\times 10^{-5}$ |
| 19 | 3.2703$\times 10^{-5}$ |
| 20 | 8.7101$\times 10^{-6}$ |
| 100 | 3.54925$\times 10^{-5}$ |
| 1000 | 1.54595$\times 10^{-5}$ |









