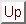


Next: The Hamilton-Jacobi Equation for
Up: Laser-driven particle mechanics
Previous: Advantage of the Hamiltonian
Contents
The most important scalar function for a dynamical system is its
dynamical phase. This phase is the (value of) the integral,
Eq.(1), evaluated for a worldline
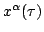 which starts at
which starts at
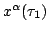 , which satisfies the Lagrange equations of motion,
and which therefore extremizes this integral. Let us designate this
extremal value by
, which satisfies the Lagrange equations of motion,
and which therefore extremizes this integral. Let us designate this
extremal value by
Figure 3:
Five different world lines
having the same starting point and terminating at points where the
dynamical phase along the world lines has reached the value 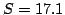 .
The locus of such termination points of such world lines with common
starting point
.
The locus of such termination points of such world lines with common
starting point 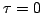 forms the isogram of a scalar function
forms the isogram of a scalar function
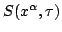 , the dynamical phase (``Hamilton-Jacobi function'')
of the Hamiltonian system.
, the dynamical phase (``Hamilton-Jacobi function'')
of the Hamiltonian system.
![\includegraphics[scale=.75]{dynamical_phase_front.eps}](img74.png) |
This integral is a function of the worldline's termination point which
we take to be
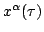 . If there is only one worldlines between
. If there is only one worldlines between
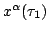 and
and
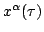 , as is usually the case, the
, as is usually the case, the
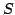 is a single valued function of the termination point.
This is depicted in Figure 3. (If there
were several such worldlines, then
is a single valued function of the termination point.
This is depicted in Figure 3. (If there
were several such worldlines, then  would be multivalued.) Thus
would be multivalued.) Thus 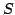 is a
function of the location
is a
function of the location
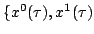 ,
, 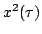 ,
,
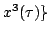 of that termination point. It also is a function of the
parameter
of that termination point. It also is a function of the
parameter 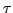 which one uses to parametrize the worldline. Thus
one has
which one uses to parametrize the worldline. Thus
one has



Next: The Hamilton-Jacobi Equation for
Up: Laser-driven particle mechanics
Previous: Advantage of the Hamiltonian
Contents
Ulrich Gerlach
2005-11-07
![]() which starts at
which starts at
![]() , which satisfies the Lagrange equations of motion,
and which therefore extremizes this integral. Let us designate this
extremal value by
, which satisfies the Lagrange equations of motion,
and which therefore extremizes this integral. Let us designate this
extremal value by
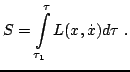
![\includegraphics[scale=.75]{dynamical_phase_front.eps}](img74.png)