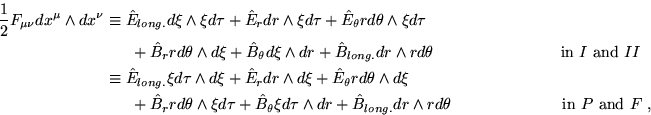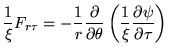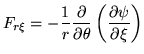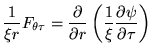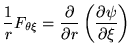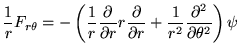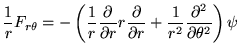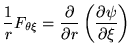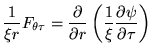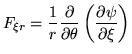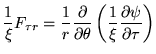

Next: The T.M. Field
Up: Application to Accelerated and
Previous: Application to Accelerated and
The T.E. Field
For the T.E. degrees of freedom the charge-current 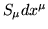 and
the vector potential
and
the vector potential 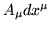 have the form given by
have the form given by
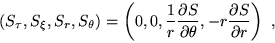 |
(29) |
and
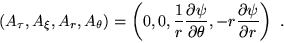 |
(30) |
The electromagnetic field,
has the following components:
The carets in the first column serve as a reminder that these
components are relative to the orthonormal basis of the metric,
Eqs.(25) and (26).
Ulrich Gerlach
2001-10-09