


Next: The T.E. Field
Up: MAXWELL FIELDS: TRANSVERSE ELECTRIC
Previous: Historical Remarks
A key virtue of splitting spacetime according to the 2+2 scheme is its
flexibility. It accommodates the necessary Rindler coordinate
geometries which are called for by the physical problem: accelerated
frames for the accelerated sources, and expanding inertial frames for
the inertial observers who measure the radiation emitted from these
sources. These geometries are
and
In these two frames the Rindler/polar-coordinatized version of
Eq.(5) is
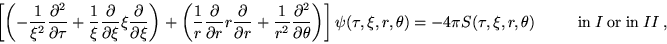 |
(27) |
and
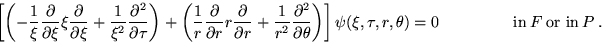 |
(28) |
Notational rule: The Rindler coordinates listed in the
arguments of the scalar functions in Eqs.(27) and (28) are
always listed with the timelike coordinate first, followed by the
spatial coordinates. Thus
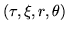 implies that the
function is defined on Rindler sectors
implies that the
function is defined on Rindler sectors  or
or 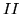 , as in
Eq.(27). On the other hand,
, as in
Eq.(27). On the other hand,
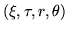 implies that the domain of the function is
implies that the domain of the function is
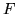 or
or 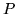 , as in Eq.(28).
, as in Eq.(28).
The feature common to the T.E. and the T.M. field is that both
of them are based on the two-dimensional curl of a scalar, say 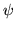 .
The difference is that for the T.E. field this curl is in the Euclidean plane,
.
The difference is that for the T.E. field this curl is in the Euclidean plane,
while for the T.M. field this curl is the Lorentz plane,
and
The 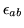 and
and 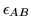 are the components of the
antisymmetric area tensors on the two respective planes.
are the components of the
antisymmetric area tensors on the two respective planes.
Subsections



Next: The T.E. Field
Up: MAXWELL FIELDS: TRANSVERSE ELECTRIC
Previous: Historical Remarks
Ulrich Gerlach
2001-10-09
![]() .
The difference is that for the T.E. field this curl is in the Euclidean plane,
.
The difference is that for the T.E. field this curl is in the Euclidean plane,