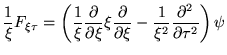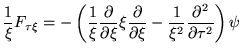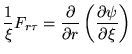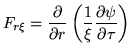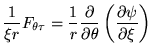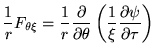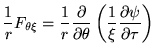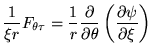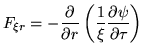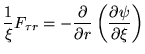

Next: A Mnemonic Short Cut
Up: Application to Accelerated and
Previous: The T.E. Field
The T.M. has its source and vector potential four-vectors lie strictly
in the 2-d Lorentz plane:
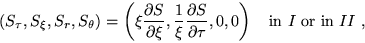 |
(31) |
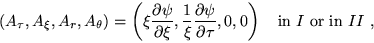 |
(32) |
and
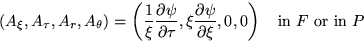 |
(33) |
The components of the T.M. Maxwell field are
Ulrich Gerlach
2001-10-09