


Next: The Rindler Interferometer
Up: RADIATION: PHYSICAL RELATION TO
Previous: Spatial Structure of the
Double Slit Interference
The third property of the radiation process is that it highlights the
interference between the waves coming from Rindler sectors  and
and
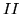 . The interference pattern, which is recorded on a hypersurface of
synchronous time
. The interference pattern, which is recorded on a hypersurface of
synchronous time 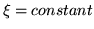 , has fringes whose separation
yields the separation between the two localized in
, has fringes whose separation
yields the separation between the two localized in  and
and 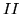 .
Let these sources be located symmetrically at
.
Let these sources be located symmetrically at
and let them have equal proper frequency 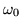 and hence (in
compliance with the first term of the wave Eq.(27) equal Rindler coordinate frequency
and hence (in
compliance with the first term of the wave Eq.(27) equal Rindler coordinate frequency
Consequently, they are characterized by their amplitudes and their
phases. Indeed, their form is
Thus the full scalar field, Eq.(54), expresses two waves. Both propagate in the expanding
inertial frame, which is coordinatized by
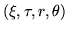 . Their
respective wave crests are located in compliance with the constant
phase conditions
. Their
respective wave crests are located in compliance with the constant
phase conditions
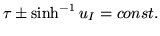 Consequently, one wave
travels into the
Consequently, one wave
travels into the 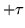 -direction with amplitude
-direction with amplitude 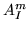 , the other
into the
, the other
into the 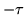 -direction with amplitude
-direction with amplitude 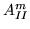 . They have well-determined phase velocities.
Together, these two waves form an interference pattern of standing waves,
. They have well-determined phase velocities.
Together, these two waves form an interference pattern of standing waves,
The amplitude of this interference pattern is 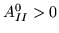 ,
and there is a uniform background of amplitude
,
and there is a uniform background of amplitude
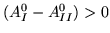 .
At synchronous time
.
At synchronous time 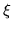 the interference fringes along the
the interference fringes along the 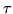 -direction
can be read off the factor
-direction
can be read off the factor
in Eq.(56). Consequently, the fringes are
spaced by the amount
This means that, analogous to a standard optical interference pattern,
the fringe spacing is inversely proportional to the distance 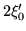 between the two sources. Furthermore, the position of this
interference pattern depends on the phase of source
between the two sources. Furthermore, the position of this
interference pattern depends on the phase of source  relative to
source
relative to
source 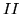 [#!phase!#]. It is difficult to find a more welcome way
than the four Rindler sectors for double slit interference.
[#!phase!#]. It is difficult to find a more welcome way
than the four Rindler sectors for double slit interference.
These observations lead to the conclusion that (i) the four Rindler
sectors quite naturally accommodate a double slit
interferometer, and that (ii) the spatial as well as the temporal
properties of the interference fringes, together with the magnitude of
the travelling background wave, are enough to reconstruct every aspect
of the two sources, Eq.(55).



Next: The Rindler Interferometer
Up: RADIATION: PHYSICAL RELATION TO
Previous: Spatial Structure of the
Ulrich Gerlach
2001-10-09
