Flow of Radiant T.M. Field Energy

The mathematical computation leading from Eq.(65) and ending with Eq.(69) can be extended without any effort to T.M. radiation. The extension consists of replacing a T.E. source with a corresponding T.M. source,

$$\frac{1}{\xi'}\frac{\partial q}{\partial\tau'}\pi a^2 \rightarrow qa~,$$

or equivalently

$$\textbf{m} \rightarrow \textbf{d}~.$$

Consequently, the formula for the flow of T.M. radiant energy due to an electric dipole subject to uniform linear acceleration 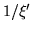$1/\xi'$ is

$${\mathcal I}_{T.M.}= (\pm)~\frac{\xi'^2}{\xi^2} \frac{2}{3} ... ...ac{1}{\xi'^2}\left(\frac{d \textbf{d}}{dt'}\right)^2 \right]~.$$ (70)

The justification for this extension is Eqs.(58) and (34). They are the same for T.E. and T.M. radiation. The radiation intensity expressed by Eq.(70) extends the familiar Larmor formula for radiation from an inertially moving electric dipole [#!Landau1962!#] to one which is accelerated linearly and uniformly.