


Next: Flow of Radiant T.M.
Up: RADIATED POWER
Previous: Electric Dipole and its
Any loop antenna radiates only for a finite amount of
time. Consequently, one can calculate the flow of total emitted
energy, which is given by the spatial integral, Eq.(57). The fact that 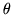 is a cyclic coordinate for axially
symmetric sources and radiation implies that
is a cyclic coordinate for axially
symmetric sources and radiation implies that
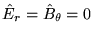 for the T.E. field. Consequently, the spatial integral, a
conserved quantity independent of time
for the T.E. field. Consequently, the spatial integral, a
conserved quantity independent of time 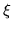 , reduces with the help of
the table of derivatives in Section IV to
, reduces with the help of
the table of derivatives in Section IV to
The computation leading to the last line has been consigned to the
Appendix. This computed quantity is the total energy flow (energy
 velocity), or equivalently, the total momentum into the
velocity), or equivalently, the total momentum into the
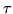 -direction, radiated by a magnetic dipole accelerated uniformly
in Rindler sector
-direction, radiated by a magnetic dipole accelerated uniformly
in Rindler sector  (upper sign) or in Rindler sector
(upper sign) or in Rindler sector 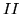 (lower
sign).
(lower
sign).
The full scalar radiation field
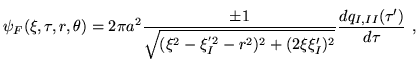 |
|
|
(67) |
with
is a linear functional correspondence. It maps the temporal history
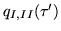 at
at
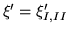 in Rindler sector
in Rindler sector  (resp.
(resp. 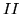 ) with 100% fidelity onto a readily measurable e.m. field
along the
) with 100% fidelity onto a readily measurable e.m. field
along the 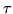 -axis (or a line parallel to it) on the spatial
hypersurface
-axis (or a line parallel to it) on the spatial
hypersurface 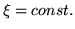 in Rindler sector
in Rindler sector 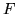 . This correspondence
has 100% fidelity because, aside from a
. This correspondence
has 100% fidelity because, aside from a 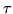 -independent factor,
the source history
-independent factor,
the source history
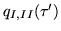 and the scalar field
and the scalar field
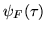 differ only by a constant
differ only by a constant 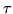 -independent shift
on their respective domains
-independent shift
on their respective domains
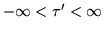 and
and
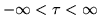 . This implies that
. This implies that
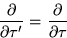 |
(68) |
when applied to the source function 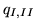 . The expression for the
radiated momentum becomes more transparent physically if one uses
the proper time derivative
. The expression for the
radiated momentum becomes more transparent physically if one uses
the proper time derivative
at the source. Introduce the (proper) magnetic moment
of the current loop having radius 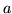 :
:
One finds from Eq.(66) that the proper radiated
longitudinal momentum (i.e. physical, a.k.a. orthonormal, component of
energy flow pointing into the 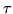 -direction) measured per proper
spatial
-direction) measured per proper
spatial 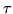 -interval
-interval 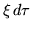 in
in 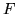 is
is
![\begin{displaymath}
{\mathcal I}_{T.E.}=
(\pm)~\frac{\xi'^2}{\xi^2} \frac{2}{3}\...
...ac{1}{\xi'^2}\left(\frac{d \textbf{m}}{dt'}\right)^2 \right]~.
\end{displaymath}](img358.png) |
(69) |
This is the formula for the proper radiant energy flow due to a magnetic dipole
moment subject to uniform linear acceleration 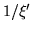 .
There are two factors of
.
There are two factors of 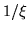 . The the first converts the coordinate
. The the first converts the coordinate
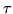 -momentum component into its physical component. The second is due
to the fact that Eq.(69) expresses this quantity
per proper distance into the
-momentum component into its physical component. The second is due
to the fact that Eq.(69) expresses this quantity
per proper distance into the 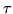 direction.
direction.
When the
acceleration 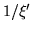 is small then the second term becomes small compared to
the first. In fact, one recovers the familiar Larmor
formula [#!Landau1962!#] relative to a static inertial frame
by letting
is small then the second term becomes small compared to
the first. In fact, one recovers the familiar Larmor
formula [#!Landau1962!#] relative to a static inertial frame
by letting 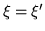 and letting
and letting
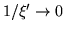 , which
corresponds to inertial motion. By contrast, Eq.(69) is the correct formula for an accelerated dipole
moment. However, observation of radiation from such a source entails
that the measurements be made relative to an expanding inertial
reference frame.
, which
corresponds to inertial motion. By contrast, Eq.(69) is the correct formula for an accelerated dipole
moment. However, observation of radiation from such a source entails
that the measurements be made relative to an expanding inertial
reference frame.



Next: Flow of Radiant T.M.
Up: RADIATED POWER
Previous: Electric Dipole and its
Ulrich Gerlach
2001-10-09
![]() is a cyclic coordinate for axially
symmetric sources and radiation implies that
is a cyclic coordinate for axially
symmetric sources and radiation implies that
![]() for the T.E. field. Consequently, the spatial integral, a
conserved quantity independent of time
for the T.E. field. Consequently, the spatial integral, a
conserved quantity independent of time ![]() , reduces with the help of
the table of derivatives in Section IV to
, reduces with the help of
the table of derivatives in Section IV to
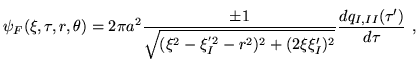
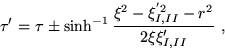
![]() is small then the second term becomes small compared to
the first. In fact, one recovers the familiar Larmor
formula [#!Landau1962!#] relative to a static inertial frame
by letting
is small then the second term becomes small compared to
the first. In fact, one recovers the familiar Larmor
formula [#!Landau1962!#] relative to a static inertial frame
by letting ![]() and letting
and letting
![]() , which
corresponds to inertial motion. By contrast, Eq.(69) is the correct formula for an accelerated dipole
moment. However, observation of radiation from such a source entails
that the measurements be made relative to an expanding inertial
reference frame.
, which
corresponds to inertial motion. By contrast, Eq.(69) is the correct formula for an accelerated dipole
moment. However, observation of radiation from such a source entails
that the measurements be made relative to an expanding inertial
reference frame.