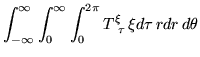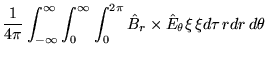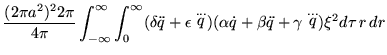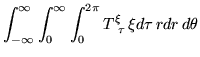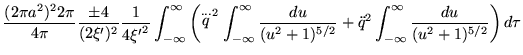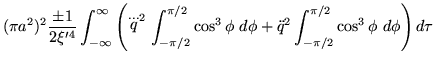Next: About this document ...
Up: APPENDIX: POTENTIAL, FIELD AND
Previous: Field Components
Being generated by a circular loop, the density of radiated momentum
pointing into the 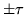 direction is independent of the polar
angle
direction is independent of the polar
angle 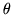 . Consequently, that density's spatial integral,
Eq.(66), reduces to
. Consequently, that density's spatial integral,
Eq.(66), reduces to
The 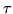 -integration affects only the dotted factors, and they
vanish outside a sufficiently large
-integration affects only the dotted factors, and they
vanish outside a sufficiently large 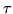 -interval, i.e.
-interval, i.e.
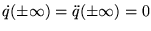 . Consequently, integration by parts
yields
. Consequently, integration by parts
yields
and
Thus there remain only three non-zero terms in the integral,
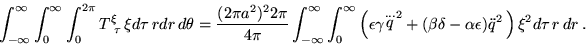 |
(87) |
The coefficients of the squared terms are
We now take advantage of the fact that the integral,
Eq.(87), is independent of the
synchronous time 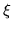 . This simplifies the evaluation of the integral
considerably because one may assume
. This simplifies the evaluation of the integral
considerably because one may assume
without changing the value of the integral. The final outcome is that (i) in each of
the expressions, Eqs.(88)-(90),
only the last term contributes to the 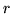 -integral and (ii) the integral
assumes a simple mathematical form if one introduces
-integral and (ii) the integral
assumes a simple mathematical form if one introduces
as the new integration variable. With this scheme one has
The to-be-used integrands have the form
both of which are always less than one in absolute value, even when
they get multiplied by 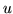 . Consequently, one is perfectly justified
in saying that
. Consequently, one is perfectly justified
in saying that
Taking note that only the last terms of Eqs.(88)-(90) give nonzero contribution, apply
the limiting form,
Eq.(92), to evaluate the integral,
Eq.(87). One finds that
The value of the integral
implies that the final result is
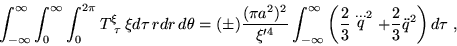 |
(94) |
the total momentum into the 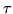 -direction radiated by a
magnetic dipole accelerated in Rindler sector
-direction radiated by a
magnetic dipole accelerated in Rindler sector  (upper sign) or in
Rindler sector
(upper sign) or in
Rindler sector 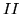 (lower sign). This is the result stated by
Eq.(66)
(lower sign). This is the result stated by
Eq.(66)



Next: About this document ...
Up: APPENDIX: POTENTIAL, FIELD AND
Previous: Field Components
Ulrich Gerlach
2001-10-09
![]() direction is independent of the polar
angle
direction is independent of the polar
angle ![]() . Consequently, that density's spatial integral,
Eq.(66), reduces to
. Consequently, that density's spatial integral,
Eq.(66), reduces to