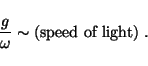
If the scatterer or radiation source is accelerated linearly and uniformly, then the standard approach is to characterize its coaccelerating coordinate frame in terms of a one-parameter family of instantaneous Lorentz frames, any one of which provides the necessary ``in'' and ``out'' or ``far-field'' regions for the measurements of the scattered and emitted radiation.
However, suppose the acceleration is extreme, i.e.
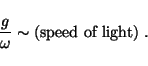
First of all, there is the distortion problem. Relative to any Lorentz frame a signal emitted by, say, an accelerated dipole would be subjected to a time-dependent Doppler shift (``Doppler chirp''). The received signal starts out with an extreme blue shift and finishes with an extreme red shift. Such a distortion prevails not only in the time domain, but also in the spatial domain of that Lorentz frame. Once this distorted signal has been acquired by the observer in his Lorentz frame, he is confronted with the task of applying a time and/or space transformation to remove this distortion. He must reconstruct the signal in order to recover with 100% fidelity the original signal emitted by the source. Such a task is tantamount to changing from his familiar set of clocks and meter rods, which make up his Lorentz frame, to a new set of clocks and units of length relative to which the signal presents itself in undistorted form with 100% fidelity.
Second, there is the problem of the trajectory of the accelerated
source. In order to have a ``far field'' region, the source must be
much smaller than one wavelength. If the acceleration lasts long
enough, the source will reach within one oscillation the
asymptotically distant observer where the measuring equipment is
located and thus vitiate its status as being located in the ``far
field'' region: there no longer is large sphere that surrounds the
source![[*]](footnote.png) .
.
Finally, during such an acceleration process the source would be
emitting plenty of information about itself (in the form of spectral
power, angular distribution, etc.). However, to acquire this
information the Maxwell field must be measured in the radiation zone.
It lies outside a sphere centered around the source with radius one
wave length. (Inside this sphere the radiation field is inextricably
mixed up with the ``induction'' field.) Measuring the Maxwell field
consists of relating its measured amplitude to the synchronized clocks
and measuring rods. But this is precisely what cannot be done if the
wavelength is larger than (acceleration)![]() of the accelerated
source. In that case the far field falls outside the semi-infinite
domain Misner et al. (1973a) where the events are characterized uniquely by
the clocks that are synchronized with the accelerated clock of the
source. Put differently, the semi-finite size of the ``local
coordinate system of the accelerated source'' Misner et al. (1973b) does not
allow an observer to distance himself far enough from the source to
identify the radiative field in the far zone.
of the accelerated
source. In that case the far field falls outside the semi-infinite
domain Misner et al. (1973a) where the events are characterized uniquely by
the clocks that are synchronized with the accelerated clock of the
source. Put differently, the semi-finite size of the ``local
coordinate system of the accelerated source'' Misner et al. (1973b) does not
allow an observer to distance himself far enough from the source to
identify the radiative field in the far zone.
Aside from removing the above ambiguities, the purpose of this note is
to identify the spacetime framework which accommodates Maxwell's field
equations applied to a uniformly and linearly accelerated radiation
source. One such application is the radiation observed in response to
a dipole source. The observed radiation rate is given by the familiar
Larmor formula but augmented due to the unique source-induced
spacetime framework. This enhanced Larmor radiation formula is the
result of a straightforward calculation based on this
framework. There are no arbitrary hypotheses. The formula is given by
Gerlach (2001):
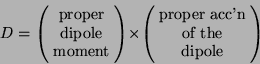
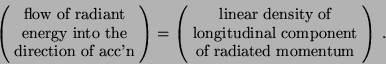

What is the spacetime framework, i.e. the nature of the arrangement of measuring rods and clocks which makes this formula possible? Even if the spacetime framework for the accelerated dipole source is clear, comprehending Eq.(1) entails asking: (i) What is the spacetime framework for the observer who measures the radiation? (ii) What is the relationship between his framework and that of the source?
As depicted in Figure 1, the source traces out a world line which is hyperbolic relative to a globally free-float observer, one with a system of inertial clocks in a state of relative rest to one another. However, the observed energy given by Eq.(1) is to be measured by a different observer, one whose clocks, even though also inertial, have nonzero expansion relative to one another.
We shall find that the arrangement of clocks and rods of such an
observer is confined to future sector ![]() of Figure 1. This sector is separated by the history of a one-way
membrane (``event horizon'') from the spacetime domain, sector
of Figure 1. This sector is separated by the history of a one-way
membrane (``event horizon'') from the spacetime domain, sector ![]() , of
the source. The purpose of this article is to establish a physical
bridge between the two, and bolt them together into a single arena
appropriate for the measurement of attributes of bodies subjected to
extreme acceleration, Eq.(1) being
one of them.
, of
the source. The purpose of this article is to establish a physical
bridge between the two, and bolt them together into a single arena
appropriate for the measurement of attributes of bodies subjected to
extreme acceleration, Eq.(1) being
one of them.
![\includegraphics[scale=.8,bb=100 440 600
720]{four_rindlerssctors_fig1old.ps}](img30.png) |
The above questions do not deal with the inertia of bodies, nor with
the dynamics of material particles, nor with the dynamics of the
Maxwell field equations![[*]](footnote.png) . Instead, they address kinematical aspects of the source
and the observer by introducing geometrical clocks which are
commensurable.
. Instead, they address kinematical aspects of the source
and the observer by introducing geometrical clocks which are
commensurable.