- ...
KINEMATICS
![[*]](footnote.png)
- With hearty felicitations to Jacob Bekenstein, the
father of black hole entropy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](footnote.png)
- To appear in ``Thirty Years of
Black Hole Entropy'', a special issue of Foundations of Physics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
source
![[*]](footnote.png)
- This difficulty might not be of much bother to the
physicist who can find sources which are subject to extreme
acceleration but which cease to exist well before they reach him.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](footnote.png)
- As far as can
be ascertained, the four acceleration-induced sectors
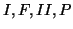 and their
respective coordinates were first introduced by Bondi in Trautman et al. (1965)
and independently by Rindler in Rindler (1966)
and their
respective coordinates were first introduced by Bondi in Trautman et al. (1965)
and independently by Rindler in Rindler (1966)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](footnote.png)
- As far as can
be ascertained, the four acceleration-induced sectors
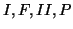 and their
respective coordinates were first introduced by Bondi in Trautman et al. (1965)
and independently by Rindler in Rindler (1966)
and their
respective coordinates were first introduced by Bondi in Trautman et al. (1965)
and independently by Rindler in Rindler (1966)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equations
![[*]](footnote.png)
- Reference Gerlach (2001),
``Radiation from violently accelerated bodies'', dealt with the
dynamics of the Maxwell field equations, to which the present paper is
a sequel.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
radar
![[*]](footnote.png)
- This has been done in a highly original way by Bondi in
Trautman et al. (1965)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Rand
![[*]](footnote.png)
- ``Cognition and Measurement'',
Ch. 1 in Binswanger and Peikoff (1990)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Peikoff
![[*]](footnote.png)
- ``Concept-Formation as
a Mathematical Process'', p.81 ff in Peikoff (1993)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... length
![[*]](footnote.png)
- Geometrical clocks with with cavity
ends at relative rest (
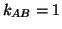 ) where first used by R.F. Marzke and
J.A. Wheeler Chiu and Hoffman (1963) and advocated by them as a standard of length.
) where first used by R.F. Marzke and
J.A. Wheeler Chiu and Hoffman (1963) and advocated by them as a standard of length.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
properties
![[*]](footnote.png)
- These three properties, reflexivity, symmetry, and
transitivity, make this relation what in mathematics is called an
equivalence relation. It divides the set of clocks into mutually
exclusive equivalence classes. In our context these classes are the
various boost-invariant sectors, whose clocks can be synchronized in each
sector. This synchronization is highlighted in Sections
V+.1667emB and V+.1667emC.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... event
![[*]](footnote.png)
- See, for example, chapter 7
in Einstein (1961) for ``a clear explanation that anyone
can understand''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
cases
![[*]](footnote.png)
- If
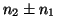 is odd, then this simply means that there
does not happen to exist a clock tick at B simultaneous with event
is odd, then this simply means that there
does not happen to exist a clock tick at B simultaneous with event
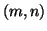 . This is, of course, due to the fact that the clock does not
furnish half-integer ticks.
. This is, of course, due to the fact that the clock does not
furnish half-integer ticks.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... next
![[*]](footnote.png)
- For a cavity with ends at relative rest, this is, in fact,
what happens in a Ti-doped sapphire laser. When turned on, usually
only one or two modes are excited. Consequently, it starts its
operation in in a continuous wave mode. However, by shining light
pulses into this laser, the lasing action starts in other cavity
modes. Since Ti-doped sapphire is a broadband amplifying medium, it is
capable of sustaining this lasing action. The superposition of these
lasing modes constitutes a light pulse bouncing back and forth inside
the cavity. This bouncing is in perfect synchrony with the external
light pulses that have been shined into the laser.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... definition
![[*]](footnote.png)
- The Doppler shift between two bodies
A and B is given by
Here 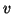 is their relative velocity, which in terms of the coordinates
of spacetime sector
is their relative velocity, which in terms of the coordinates
of spacetime sector 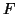 is given by
is given by
This yields
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frequencies
![[*]](footnote.png)
- For accelerated cavities one talks about temporal
frequencies, while for inertially expanding cavities one talks about
spatial frequencies, but frequencies nevertheless.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... meaning''
![[*]](footnote.png)
- Remark by E. Wigner on page 285 in the
discussion following papers by S.S. Chern and T. Regge in
Wolf (1980)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... computations].''
![[*]](footnote.png)
- Page 20 in
Schroedinger (1956)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fallacies
![[*]](footnote.png)
- One of them, the fallacy of the ``stolen concept'',
deserves special mention because of its ubiquity, even among
physicists. It is exemplified in statements such as (i) ``coordinates
are unphysical'', (ii) ``before
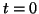 the universe did not exist''
(iii) ``the beginning of the universe'', (iv) ``the creation of the
universe'', (v) ``the birth of the universe'', (vi) ``Why does the
universe exist?'', etc.
the universe did not exist''
(iii) ``the beginning of the universe'', (iv) ``the creation of the
universe'', (v) ``the birth of the universe'', (vi) ``Why does the
universe exist?'', etc.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
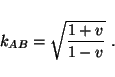
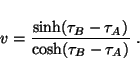
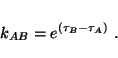
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)