


Next: Dynamical Phase as Physical
Up: Laser-driven particle mechanics
Previous: The Hamilton-Jacobi Equation for
Contents
As an example, consider the problem of solving the H-J equation for
a charged particle in the vector potential
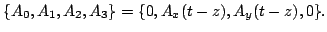 |
(12) |
It expresses a generic plane wave traveling towards positive 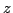 . The
H-J equation is
. The
H-J equation is
To make this equation physically more transparent and mathematically
more manageable one introduces the retarded and advanced time
coordinates
and
In terms of these the H-J equation becomes
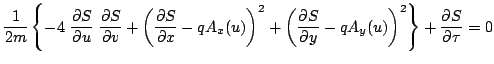 |
(13) |
This equation is readily solved by the method of separation of
variables according to which the solution,
is a sum of antiderivatives, each one depending only on
its respective integration variable. With this stipulation one finds
that the components of the gradient of 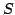 are
are
where 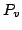 ,
, 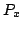 ,
, 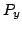 , as well as
, as well as 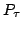 , are the constants of
separation1. Consequently, the
Hamilton-Jacobi function (``Hamilton's principal function'',
``Schroedinger phase'', dynamical phase)
, are the constants of
separation1. Consequently, the
Hamilton-Jacobi function (``Hamilton's principal function'',
``Schroedinger phase'', dynamical phase)
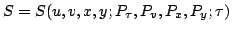 |
(19) |
has the form
or more generally
Both 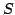 and
and 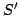 are solutions to the H-J equation, but
are solutions to the H-J equation, but 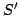 has an
additive constant
has an
additive constant
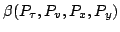 which is a function
of the four separation constants.
Although the difference between
which is a function
of the four separation constants.
Although the difference between 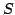 and
and 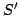 is trivial from the
perspective of solving the H-J equation, the opposite is true from the
viewpoint of physics and mathematics. Indeed, suppose one let's
Then one obtains
is trivial from the
perspective of solving the H-J equation, the opposite is true from the
viewpoint of physics and mathematics. Indeed, suppose one let's
Then one obtains
The usefulness of this H-J function  is that it generates new
phase space coordinates relative to which the solutions of Hamilton's
Eqs.(3)-(4) are straight lines. They are depicted in
Figure 8 on page
is that it generates new
phase space coordinates relative to which the solutions of Hamilton's
Eqs.(3)-(4) are straight lines. They are depicted in
Figure 8 on page ![[*]](crossref.png) . In other words, solving the H-J equation for
. In other words, solving the H-J equation for  is tantamount to solving Hamilton's equations for all possible initial
conditions.
is tantamount to solving Hamilton's equations for all possible initial
conditions.

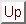


Next: Dynamical Phase as Physical
Up: Laser-driven particle mechanics
Previous: The Hamilton-Jacobi Equation for
Contents
Ulrich Gerlach
2005-11-07
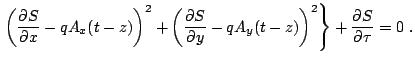
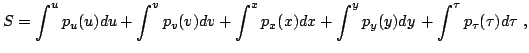
![[*]](crossref.png) . In other words, solving the H-J equation for
. In other words, solving the H-J equation for