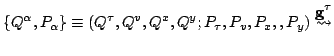


Next: Action-Angle Representation
Up: Laser-driven particle mechanics
Previous: Laser-driven Particle Mechanics via
Contents
Together with the spacetime gradient of  , Eqs.(15)-(19), the constructive interference
conditions, Eq.(23), also yields a
moving point in phase space. The starting point is
, Eqs.(15)-(19), the constructive interference
conditions, Eq.(23), also yields a
moving point in phase space. The starting point is
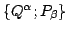 when
when
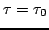 . When
. When 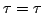 the point
has reached
the point
has reached
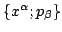 . This moving point forms a
trajectory in phase space,
. This moving point forms a
trajectory in phase space,
It is a solution to Hamilton's equations of motion, Eqs.(3)-(4).
-
Problem 4: Show that (a) the conditions for constructive interference,
Eq.(23), together with (b) the fact
that the dynamical phase
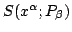 satisfies the H-J
equation, Eq.(12), imply that each phase trajectory
satisfies the Hamiltonian equations of motion, Eqs.(3) and (4).
satisfies the H-J
equation, Eq.(12), imply that each phase trajectory
satisfies the Hamiltonian equations of motion, Eqs.(3) and (4).
Hint: Differentiate the H-J equation
with respect to
each of the constants of motion 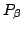 . Differentiate the four equations
for constructive interference
with respect to the world line
parameter
. Differentiate the four equations
for constructive interference
with respect to the world line
parameter 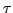 . Compare the results. Next differentiate
the H-J equation with respect to each of the coordinates
. Compare the results. Next differentiate
the H-J equation with respect to each of the coordinates 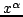 .
.
Consider the set of phase space trajectories obtained from the
dynamical phase 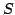 . For fixed
. For fixed 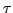 they yield the map
they yield the map
where, according to Eqs.(16)-(18)
and (24)-(27),
The relation
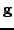 is called the phase flow generated by
the superhamiltonian
is called the phase flow generated by
the superhamiltonian
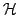 . Physically this flow expresses
the evolution of a collisionless ensemble of charged particles each
launched with its own
. Physically this flow expresses
the evolution of a collisionless ensemble of charged particles each
launched with its own
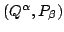 in the field of a
laser. Mathematically this flow combines two concepts into one:
letting
in the field of a
laser. Mathematically this flow combines two concepts into one:
letting 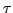 vary while keeping
vary while keeping
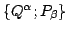 fixed yields
a phase space trajectory; letting
fixed yields
a phase space trajectory; letting
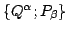 vary while
keeping
vary while
keeping 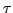 fixed yields a (canonical) transformation,
Eq.(28). Combining the two, one obtains
fixed yields a (canonical) transformation,
Eq.(28). Combining the two, one obtains
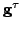 , a
, a
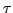 -parametrized family of transformations which expresses the
nonintersecting trajectories of a set of moving points, each one
labelled by eight coordinates.
-parametrized family of transformations which expresses the
nonintersecting trajectories of a set of moving points, each one
labelled by eight coordinates.
The geometrical representation of these transformations is depicted in
Figure 8: Points of the
intersection of the straight
trajectories with a
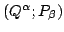 -plane in (b)
get mapped into the intersection of the curved trajectories with
a
-plane in (b)
get mapped into the intersection of the curved trajectories with
a
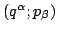 -plane in (a).
-plane in (a).
Figure 8:
Three
trajectories in the extended phase space relative to (a) the given physical coordinates
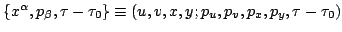 and (b) the new coordinates
and (b) the new coordinates
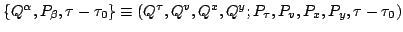 relative to which the trajectories are straight lines. The mapping
relative to which the trajectories are straight lines. The mapping
 is the phase flow map discussed in the text.
is the phase flow map discussed in the text.
![\includegraphics[scale=.5]{phase_spacetrajectories.eps}](img172.png) |
Consider the transformation corresponding to
 ,
,
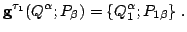 |
(28) |
Then
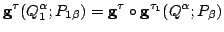 |
(29) |
is the composite of
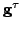 and
and
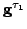 . But
both
. But
both
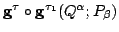 and
and
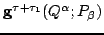 are solutions to the same
(time-independent!) Hamilton's equations of motion with the same
starting point. Consequently,
One sees that
are solutions to the same
(time-independent!) Hamilton's equations of motion with the same
starting point. Consequently,
One sees that
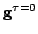 is the identity map, and
is the identity map, and
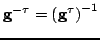 is the inverse map.
Consequently, Eq.(28) is a
is the inverse map.
Consequently, Eq.(28) is a 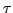 -parametrized group of
phase space coordinate transformations, the phase flow of
-parametrized group of
phase space coordinate transformations, the phase flow of
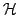 . Being generated by the dynamical phase
. Being generated by the dynamical phase 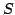 , they are
canonical transformations whose defining property is
Eq.(8).
, they are
canonical transformations whose defining property is
Eq.(8).
These transformations have a striking simplifying effect on the phase
space trajectories. Suppose one considers the extended
phase space,
It is (8+1)-dimensional and it is obtained from
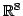 by
adding the
by
adding the 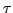 -line as an extra coordinate axis. In this space the
phase space trajectories are represented by curved non-intersecting
lines as in Figure 8(a). The
-line as an extra coordinate axis. In this space the
phase space trajectories are represented by curved non-intersecting
lines as in Figure 8(a). The
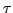 -parametrized canonical transformation constitute a map from a
-parametrized canonical transformation constitute a map from a
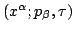 -coordinatized copy of the extended phase
space
-coordinatized copy of the extended phase
space
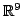 to a
to a
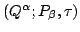 -coordinatized
copy of the same extended phase space
-coordinatized
copy of the same extended phase space
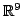 . The benefit of
the latter is that relative to it the phase space trajectories are
straightened out as in Figure 8(b).
. The benefit of
the latter is that relative to it the phase space trajectories are
straightened out as in Figure 8(b).
However, as intimated by Eq.(23), the
same constructive interference conditions also imply a
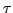 -dependent canonical coordinate transformation,
-dependent canonical coordinate transformation,
This transformation, which is given (implicitly) by Eqs.(19)-(18) and (25)-(27), is generated by the Hamilton-Jacobi
function, Eq.(20). This transformation straightens out
the phase space trajectories (as depicted in Figure 8) of Hamilton's equations of motion (3) and (4).
- Problem 5:
Write down and solve Hamilton's equations of motion,
(3)-(4), and verify that the solution coincides
with the constuctive interference condition,
Eqs.(24)-(27)



Next: Action-Angle Representation
Up: Laser-driven particle mechanics
Previous: Laser-driven Particle Mechanics via
Contents
Ulrich Gerlach
2005-11-07
![]() , Eqs.(15)-(19), the constructive interference
conditions, Eq.(23), also yields a
moving point in phase space. The starting point is
, Eqs.(15)-(19), the constructive interference
conditions, Eq.(23), also yields a
moving point in phase space. The starting point is
![]() when
when
![]() . When
. When ![]() the point
has reached
the point
has reached
![]() . This moving point forms a
trajectory in phase space,
. This moving point forms a
trajectory in phase space,
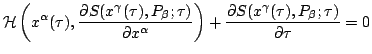
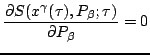
![]() . For fixed
. For fixed ![]() they yield the map
they yield the map
![]() -plane in (b)
get mapped into the intersection of the curved trajectories with
a
-plane in (b)
get mapped into the intersection of the curved trajectories with
a
![]() -plane in (a).
-plane in (a).
![\includegraphics[scale=.5]{phase_spacetrajectories.eps}](img172.png)
![]() ,
,
![]() -dependent canonical coordinate transformation,
-dependent canonical coordinate transformation,