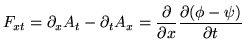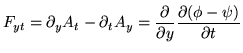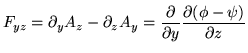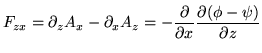Next: Existence and Uniqueness of
Up: The Method of the
Previous: The T.M. Field
There are also the T.E.M. degrees of freedom.
For them the Maxwell four-vector source
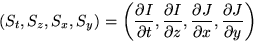 |
(14) |
is derived from two functions 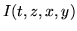 and,
and, 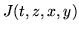 , scalars
on the 2-D Lorentz plane and the 2-D-Euclidean plane respectively. They
are, however, not independent. Charge conservation demands the
relation
, scalars
on the 2-D Lorentz plane and the 2-D-Euclidean plane respectively. They
are, however, not independent. Charge conservation demands the
relation
The T.E.M. four-vector potential
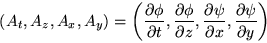 |
(15) |
has the same form, but only the difference 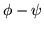 is determined
by the field equations. Indeed, the T.E.M. field components are derived from
this difference:
This e.m. field satisfies the Maxwell field equations if any two of
the following three scalar equations,
is determined
by the field equations. Indeed, the T.E.M. field components are derived from
this difference:
This e.m. field satisfies the Maxwell field equations if any two of
the following three scalar equations,
are satisfied. The last equation is, of course, simply the
conservation of charge equation. Furthermore, it is evident that the T.E.M. field
propagates strictly along the 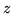 -axis, the direction of the Pointing
vector.
-axis, the direction of the Pointing
vector.



Next: Existence and Uniqueness of
Up: The Method of the
Previous: The T.M. Field
Ulrich Gerlach
2001-10-09