


Next: The T.E.M. Field Equations
Up: The Method of the
Previous: The T.E. Field
The T.M. Field
For the T.M. degrees of freedom the source and the electromagnetic
field are also derived from a solution to the same inhomogeneous
scalar wave Eq.(5). However, the difference
from the T.E. case is that the four-vector components of the source and
the vector potential lie in the Lorentz 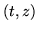 -plane. Thus, instead
of Eqs.(9) and (10), one has the T.M. source
-plane. Thus, instead
of Eqs.(9) and (10), one has the T.M. source
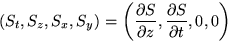 |
(11) |
and the T.M. vector potential
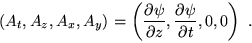 |
(12) |
All the corresponding T.M. field components are derived from the
scalar 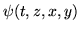 :
:
![\begin{displaymath}
\begin{array}{c}
\begin{tabular}[t]{\vert l\vert c\vert}
\h...
...ial \psi}{\partial t}$\\
[3mm]\hline
\end{tabular}\end{array}\end{displaymath}](img86.png) |
(13) |
These components are guaranteed to satisfy all the Maxwell field equations
with the T.M. source, Eq.(11), whenever 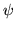 satisfies the inhomogeneous scalar wave equation, Eq.(5).
satisfies the inhomogeneous scalar wave equation, Eq.(5).
Ulrich Gerlach
2001-10-09
![]() -plane. Thus, instead
of Eqs.(9) and (10), one has the T.M. source
-plane. Thus, instead
of Eqs.(9) and (10), one has the T.M. source
![\begin{displaymath}
\begin{array}{c}
\begin{tabular}[t]{\vert l\vert c\vert}
\h...
...ial \psi}{\partial t}$\\
[3mm]\hline
\end{tabular}\end{array}\end{displaymath}](img86.png)