


Next: Historical Remarks
Up: MAXWELL FIELDS: TRANSVERSE ELECTRIC
Previous: The T.E.M. Field Equations
Can an arbitrary vector potential be written in terms of four suitably
chosen scalars
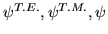 and
and 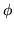 so as to
satisfy Eqs.(10),
(12), and (15)? If the answer is ``yes'' then any e.m. field
can be expressed in terms of these scalars, and one can claim that
these scalars give a complete and equivalent description of the
e.m. field. It turns out that this is indeed the case. In fact, the
description is also unique. Indeed, given the vector potential,
Eq.(7), there exist four unique scalars
which are determined by this vector potential so as to satisfy
Eqs.(10), (12), and (15). The determining equations, obtained by taking suitable
derivatives, are
so as to
satisfy Eqs.(10),
(12), and (15)? If the answer is ``yes'' then any e.m. field
can be expressed in terms of these scalars, and one can claim that
these scalars give a complete and equivalent description of the
e.m. field. It turns out that this is indeed the case. In fact, the
description is also unique. Indeed, given the vector potential,
Eq.(7), there exist four unique scalars
which are determined by this vector potential so as to satisfy
Eqs.(10), (12), and (15). The determining equations, obtained by taking suitable
derivatives, are
These equations guarantee the existence of the sought after scalar
functions
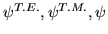 and
and 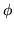 . Their uniqueness
follows from their boundary conditions in the Euclidean
. Their uniqueness
follows from their boundary conditions in the Euclidean 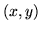 -plane
and their initial conditions in the Lorentzian
-plane
and their initial conditions in the Lorentzian
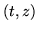 -plane. Consequently, Eqs.(19)-(22) together with Eqs.(10), (12), and
(15) establish a one-to-one
linear correspondence between the space of vector potentials and the
space of four ordered scalars,
-plane. Consequently, Eqs.(19)-(22) together with Eqs.(10), (12), and
(15) establish a one-to-one
linear correspondence between the space of vector potentials and the
space of four ordered scalars,
Of the four scalars, three are gauge invariants, namely
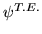 ,
, 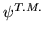 , and the difference
, and the difference 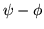 , a
result made obvious by inspecting Eqs.(19)-(22).
, a
result made obvious by inspecting Eqs.(19)-(22).



Next: Historical Remarks
Up: MAXWELL FIELDS: TRANSVERSE ELECTRIC
Previous: The T.E.M. Field Equations
Ulrich Gerlach
2001-10-09
![]() and
and ![]() so as to
satisfy Eqs.(10),
(12), and (15)? If the answer is ``yes'' then any e.m. field
can be expressed in terms of these scalars, and one can claim that
these scalars give a complete and equivalent description of the
e.m. field. It turns out that this is indeed the case. In fact, the
description is also unique. Indeed, given the vector potential,
Eq.(7), there exist four unique scalars
which are determined by this vector potential so as to satisfy
Eqs.(10), (12), and (15). The determining equations, obtained by taking suitable
derivatives, are
so as to
satisfy Eqs.(10),
(12), and (15)? If the answer is ``yes'' then any e.m. field
can be expressed in terms of these scalars, and one can claim that
these scalars give a complete and equivalent description of the
e.m. field. It turns out that this is indeed the case. In fact, the
description is also unique. Indeed, given the vector potential,
Eq.(7), there exist four unique scalars
which are determined by this vector potential so as to satisfy
Eqs.(10), (12), and (15). The determining equations, obtained by taking suitable
derivatives, are