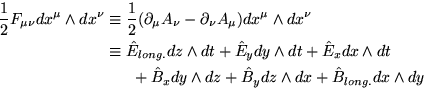The Method of the 2+2 Split

The first task is to solve the inhomogeneous Maxwell field equations[#!Candelas_plus_Higuchi!#,#!Alexander_and_Gerlach!#] and use its solution to determine the radiation properties to be measured. The best way to set up and solve these equations is to take advantage of the fact the cylindrical symmetry dictates a 2+2 decomposition of spacetime into a pair orthogonal 2-dimensional planes, one Euclidean, the other Lorentzian. The experienced reader will see that such a decomposition minimizes (compared to text book treatments) the amount of mathematical analysis, while simultaneously retaining all physical aspects of the radiation problem. Furthermore, these physical aspects lend themselves to nearly effortless identification because of the flexible curvilinear coordinate systems which the two orthogonal planes accommodate.

However, in order to appreciate the underlying line of reasoning as rapidly as possible, we first illustrate the 2+2 decomposition procedure on Minkowski spacetime coordinatized with the familiar rectilinear coordinates. We do this before proceeding to use it to solve Maxwell's equations relative to the various Rindler coordinates plus polar coordinates as called for by the cylindrical coordinate geometry of linearly accelerating bodies.

In the presence of cylindrical symmetry the Maxwell field equations decouple into two sets, each of which gives rise to its own inhomogeneous scalar wave equation

$$\left[ \left( -{\partial^2 \over \partial t^2} +{\partial^2... ...ial y^2} \right) \right] \psi(t,z,x,y) =-4\pi\, S(t,z,x,y)~~.$$ (5)

The charge-current four-vector

$$S_\mu dx^\mu=S_t dt +S_z dz +S_x dx+S_y dy$$ (6)

for each set determines and is determined by appropriate derivatives of the scalar source $S(t,z,x,y)$. Similarly, the vector potential

$$A_\mu dx^\mu =A_t dt+A_z dz+ A_x dx +A_y dy$$ (7)

as well as the electromagnetic field

$$\begin{eqnarray*} \frac{1}{2}F_{\mu\nu}dx^\mu \wedge dx^\nu &\equiv& \frac{1}{... ...B_xdy\wedge dz +\hat B_y dz\wedge dx +\hat B_{long.}dx\wedge dy \end{eqnarray*}$$

determine and are determined by the scalar wave function $\psi(t,z,x,y)$ with the result that the Maxwell field equations

$${F_\mu^{~\nu}}_{;\nu}=4\pi S_\mu$$ (8)

are satisfied whenever the wave Eq.(5) is satisfied.